13. Decision Tree - CART
16 Jan 2022- 1. Giới thiệu
- 2. Ví dụ
- 3. CART
- 4. Ý nghĩa các node trong sklearn
- 5. Xử lí Overfiting
- 6. Regression
- 7. Đánh giá và kết luận
- 8. Tham khảo
1. Giới thiệu
Ở bài 12. Decision Tree - ID3 (1/2), mình đã trình bày về thuật toán ID3 với hàm information gain dùng làm điều kiện để đưa ra quyết định chọn thuộc tính khi xây dựng một cây quyết định. Thuật toán này sẽ chỉ làm việc với dữ liệu dạng categorical (có thể chuyển từ numeric sang categorical) tuy nhiên như đã bàn luận thì cách này có thể làm mất đi tính quan trọng của dữ liệu. Vì vậy, ở bài này mình sẽ trình bày về thuật toán có thể làm việc với cả dữ liệu categorical và liên tục, đó là: CART.
CART sẽ được xây dựng một Decision Tree bằng cách ở mỗi node chỉ tạo ra 2 child node có nghĩa rằng ở thuật toán này, cây được xây dựng sẽ là một cây nhị phân (binary tree). Vì vậy các câu hỏi lúc này sẽ trở thành dạng True, False, hơn nữa với CART sẽ sử dụng một độ đo khác để tính toán độ tinh khiết của phân phối xác xuất tại non-leaf node dễ dàng hơn đó là Gini. Về phần ý tưởng thì thuật toán ID3 và CART đều sử dụng Greedy để tìm ra những thuộc tính phù hợp nhất ở mỗi lần lặp để đặt vào non-leaf node với một chỉ số đánh giá mức độ tinh khiết lần lượt là: information gain và gini. Chi tiết mình sẽ trình bày bên dưới.
2. Ví dụ
Để dễ dàng cho việc giải thích ở một số vấn đề chuyên sâu thì mình sẽ sử dụng thư viện sklearn để biểu diểu về mặt kết quả trước, sau đó mình sẽ giải thích sau. Cùng với bộ dữ liệu về thời tiết đã được sử dụng ở bài 12. Decision Tree - ID3 (1/2), tuy nhiên mình cần tiền xử lí một chút vì Decision Tree trong sklearn yêu cầu đầu vào phải là dạng số nên sẽ phải chuyển các thuộc tính dạng categorical này one-hot vector. Ta cần xử lí như sau:
1
2
3
4
import pandas as pd
df = df.drop(columns=["id"])
data = pd.get_dummies(df, columns=['outlook', 'temperature','humidity','wind'])
data
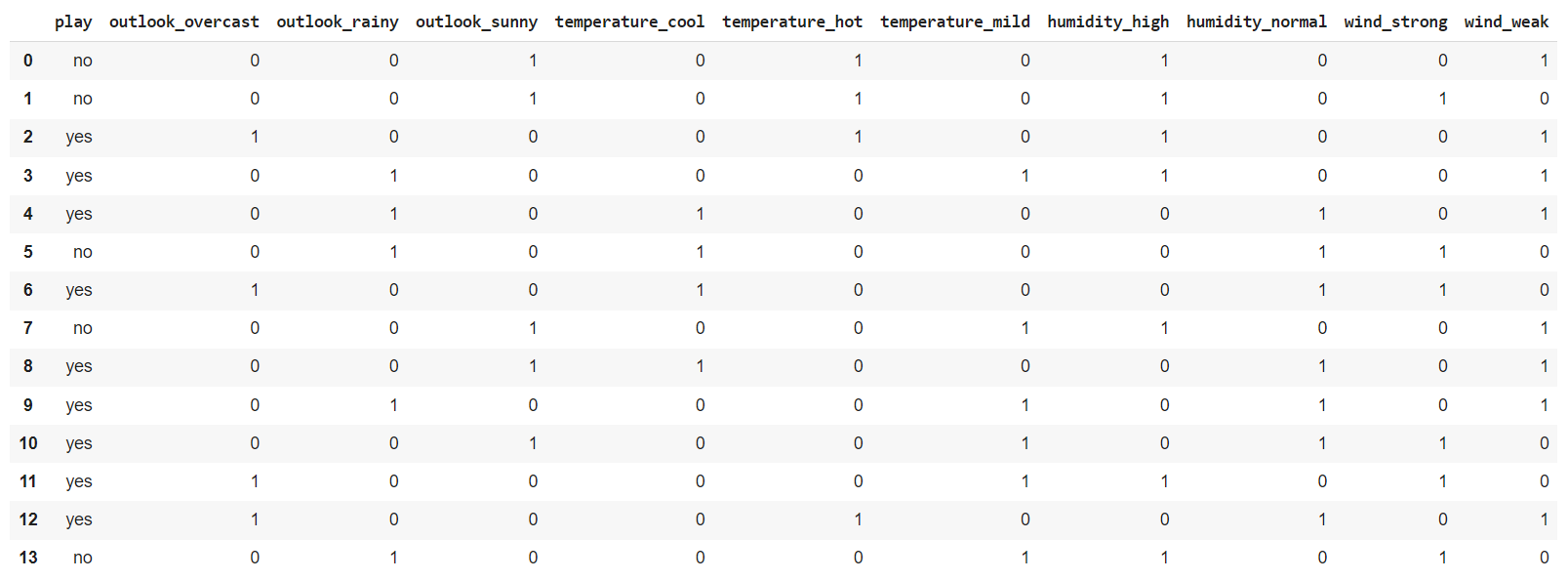
Tiếp theo ta cần xác định dữ liệu là thuộc tính và biến mục tiêu:
1
2
3
4
5
features = data.columns
target = 'play'
X = data[features].drop(columns=['play'])
y = data[target]
Cuối cùng mình sẽ import các thư viện cần thiết của sklearn để tạo nên cây quyết định dựa trên thuật toán CART:
1
2
3
4
5
6
7
8
9
10
11
import graphviz
from sklearn import tree
dot_data = tree.export_graphviz(tree_clf, out_file=None,
feature_names=X.columns,
class_names=['No','Yes'],
rounded=True,
filled=True)
graph = graphviz.Source(dot_data, format="png")
graph
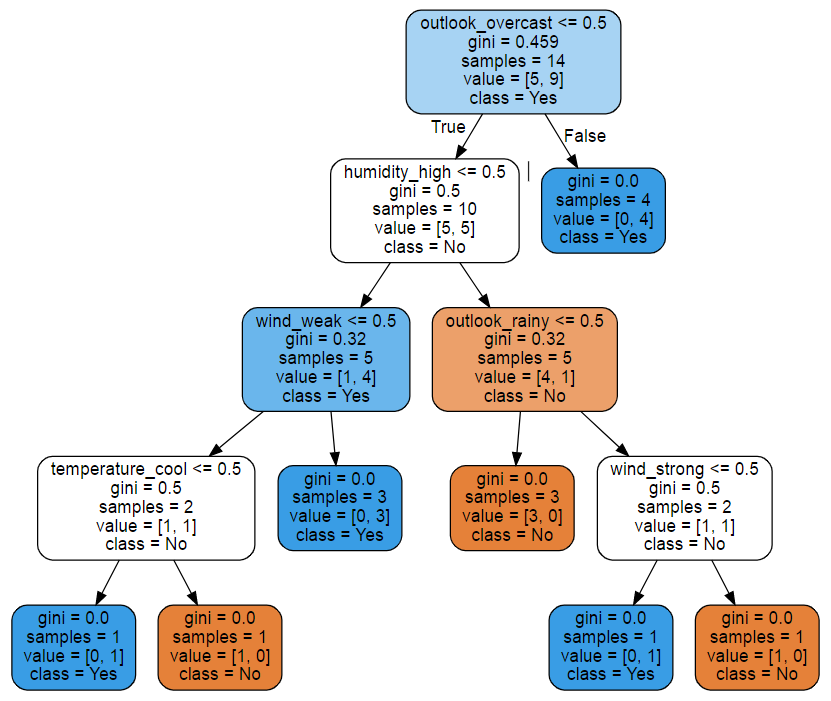
Như đã đề cập bên trên thì thuật toán CART sẽ tạo ra một cây nhị phân. Nếu bạn để ý thì các leaf-node lúc này đều có một giá trị gini = 0.0 đây chính là cách mà thuật toán CART lựa chọn thuộc tính (chi tiết mình sẽ trình bày bên dưới). Với cây ta đã tạo được, đảm bảo rằng kết quả dự đoán trên training data sẽ chính xác 100% giống với ID3. Bây giờ nếu cần dự đoán một dữ liệu mới ta chỉ cần đi hỏi liên tiếp các câu hỏi cho tới khi non-leaf node xuất hiện, cụ thể mình sẽ kiểm tra như sau:
-
Cố định 3 thuộc tính
outlook != overcast, humidity = normal, wid = weak -
Các thuộc tính khác sẽ được chọn ngẫu nhiên
-
Đưa ra dự đoán 10 lần với cách lựa chọn trên
1
2
3
4
5
6
7
8
9
10
11
12
13
14
import random as rd
for i in range(10):
outlook = rd.choice(['sunny','rainy'])
temperature = rd.choice(['hot','mild','cold'])
x = pd.DataFrame({'outlook':outlook, 'temperature':temperature, 'humidity':['normal'], 'wind':['weak']})
x = pd.get_dummies(x, columns=['outlook', 'temperature','humidity','wind'])
x_new = pd.DataFrame(np.zeros((1, X.shape[1])), columns=X.columns)
x_new[x == 1] = x
y_pred = tree_clf.predict_proba(x_new)[0]
label = tree_clf.predict(x_new)[0]
print('probability no {}, yes {}'.format(y_pred[0], y_pred[1]))
print('predicted label {}'.format(label))
Kết quả hoàn toàn giống nhau:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
probability no 0.0, yes 1.0
predicted label yes
probability no 0.0, yes 1.0
predicted label yes
probability no 0.0, yes 1.0
predicted label yes
probability no 0.0, yes 1.0
predicted label yes
probability no 0.0, yes 1.0
predicted label yes
probability no 0.0, yes 1.0
predicted label yes
probability no 0.0, yes 1.0
predicted label yes
probability no 0.0, yes 1.0
predicted label yes
probability no 0.0, yes 1.0
predicted label yes
probability no 0.0, yes 1.0
predicted label yes
Điều này là hoàn toàn chính xác, nếu bạn nhìn lại cây mà ta đã tạo được thì dự đoán này sẽ chỉ đi theo 1 nhánh màu xanh như sau:
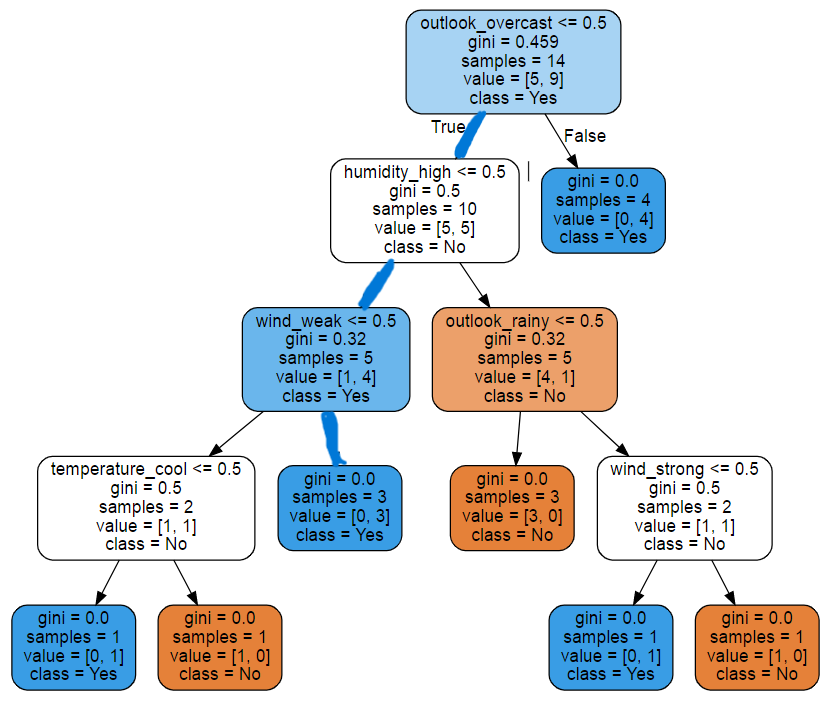
Tới đây là cách cơ bản để tạo một Decision Tree dựa trên thuật toán CART trong sklearn. Nếu bạn chưa hiểu cơ bản cách mà Decision Tree hoạt động và tạo nên như thế nào thì bạn có thể đọc lại bài bài 12. Decision Tree - ID3 (1/2) mình đã trình bày chi tiết. Vậy với Decision Tree được tạo nên bởi thuật toán CART sử dụng độ đo tinh khiết là Gini được làm như thế nào? Mình sẽ trình bày cụ thể bên dưới.
3. CART
Để hiểu rõ mặt bản chất của phương pháp sử dụng Gini làm thước đo độ tinh khiết, ở phần này mình sẽ trình bày lại một chút về mặt toán học (bất đẳng thức) một vấn đề rất hay của bậc THCS.
3.1. Bất đẳng thức Cauchy - Schwarz (Bunyakovsky)
Cho các số thực $(a_1, a_2, a_3, …, a_n)$ và $(b_1, b_2, b_3, …, b_n)$ với $n \geq 2$, ta có bất đẳng thức sau:
\[(a_1^2 + a_2^2 + a_3 + ... + a_n^2)(b_1^2 + b_2^2 + b_3^2 + ... + b_n^2) \geq (a_1b_1 + a_2b_2 + a_3b_3 + ... + a_nb_n)^2\]Chứng minh:
Đặt:
\[A = a_1^2 + a_2^2 + a_3 + ... + a_n^2\] \[B = b_1^2 + b_2^2 + b_3 + ... + b_n^2\] \[C = a_1b_1 + a_2b_2 + a_3b_3 + ... + a_nb_n\]Xét giá trị $x$ là một số thực bất kì ta luôn có:
\[(a_1x - b_1)^2 \geq 0\] \[<=> a_1^2x^2 - 2a_1xb_1 + b_1^2 \geq 0\]Tương tự vẫn xét giá trị $x$ này với các giá trị $(a_1, a_2, … a_n)$ và $(b_1, b_2,… b_n)$, rồi cộng vế ta được:
\[(a_1^2 + a_2^2 + a_3 + ... + a_n^2)x^2 - 2x(a_1b_1 + a_2b_2 + ... + a_nb_n) + (b_1^2 + b_2^2 + b_3 + ... + b_n^2) \geq 0 \quad \quad (1)\]Xét giá trị $x = \frac{C}{A}$ và thế $x, A, B, C$ vào bất đẳng (1) suy ra:
\[A\frac{C^2}{A^2} - 2\frac{C^2}{A} + B \geq 0\] \[<=> B - \frac{C^2}{A} \geq 0\] \[<=> AB \geq C^2 (\text{dpcm})\]Xét với $b_1 = b_2 = b_3 = … = b_n = 1$ thì bất đẳng thức lúc này trở thành:
\[(a_1^2 + a_2^2 + a_3 + ... + a_n^2)n \geq (a_1 + a_2 + a_3 + ... + a_n)^2 \quad \quad (2)\]Ngoài ra có một bất đẳng thức:
\[a_1^2 + a_2^2 + a_3 + ... + a_n^2 \leq (a_1 + a_2 + a_3 + ... + a_n)^2 \quad \quad (3)\]3.2. Gini index
Gini index tương tự như information gain mà mình đã trình bày ở bài 12. Decision Tree - ID3 (1/2), dùng để đánh giá xem việc phân chia ở node điều kiện có tốt hay không. Tuy nhiên, đầu tiên ta sẽ cần tính toán chỉ số Gini ở mỗi node.
Bước 1: Xét bài toán phân loại có $C$ class, node đang tới là một non-leaf node $\mathcal{p}$ với các điểm dữ liệu tạo thành là $\mathcal{S}$ có số lượng phần tử là $N$. $N_i$ là số lượng phần tử của class $i$ với $i = 1, 2, …, C$. Xác suất để mỗi điểm dữ liệu rơi vào một class $i$ được xấp xỉ bằng $\frac{N_i}{N} = p_i => \sum_{i=1}^C p_i = 1$. Chỉ số này được tính bằng cách lấy 1 trừ đi tổng bình phương phân phối xác suất ở mỗi lớp, như sau:
\[\mathbf{\text{Gini}(\mathcal{S})} = 1-\sum_{i=1}^{C} p_i^2 \quad\quad (4)\]Dựa vào (3) suy ra: $\sum_{i=1}^{C}p_i^2 \leq (\sum_{i=1}^{C} p_i)^2 =>\sum_{i=1}^{C}p_i^2 \leq 1 \quad (4) => \mathbf{\text{Gini}(\mathbf{S})} \geq 0$ và dấu ‘=’ xảy ra khi và chỉ khi tồn tại một giá trị $p_i = 1$ (nhãn thuộc về một lớp duy nhất).
Dựa vào (2) suy ra: $\sum_{i=1}^{C}p_i^2 \geq \frac{(\sum_{i=1}^{C} p_i)^2}{C} =>\sum_{i=1}^{C}p_i^2 \geq \frac{1}{C} => \mathbf{\text{Gini}(\mathbf{S})} \leq \frac{C-1}{C}$ và dấu ‘=’ xảy ra khi và chỉ khi $p_i = \frac{1}{C}$ với mọi $i = 1, 2, …, C$ (phân phối nhãn của các lớp đang chia đều).
Bước 2: Sau khi đã tính toán được giá trị Gini cho non-leaf node $\mathcal{p}$, ta cần chọn ra một thuộc tính $x$. Và khi $x$ được chọn thì nhánh tiếp theo sẽ có số lượng child node bằng với số giá trị mà thuộc tính $x$ có. Dựa trên $x$, các điểm dữ liệu trong $\mathcal{S}$ được phân ra thành $K$ child node $\mathcal{S_1},\mathcal{S_2},…,\mathcal{S_K}$ với số điểm trong mỗi child node lần lượt là $m_1,m_2,…,m_K$. Suy ra tổng trọng số Gini của mỗi child node là:
\[\mathbf{\text{Gini}}(x, \mathcal{S}) = \sum_{k=1}^K \frac{m_k}{N} \mathbf{\text{Gini}}(\mathcal{S}_k) \quad\quad (5)\]Thông số đánh giá Gini index dựa trên thuộc tính $x$ được tính toán như sau:
\[\mathbf{\text{G}}(x, \mathcal{S}) = \mathbf{\text{Gini}(\mathcal{S})} - \mathbf{\text{Gini}}(x, \mathcal{S})\]Cuối cùng, thuộc tính được lựa chọn $x^*$ là:
\[x^* = \arg\max_{x} \mathbf{G}(x, \mathcal{S}) = \arg\min_{x} \mathbf{\text{Gini}}(x, \mathcal{S})\]tức $x^*$ làm cho Gini index lớn nhất hoặc tổng trọng số Gini nhỏ nhất
Bước 3: Bước 1 và Bước 2 được lặp lại cho tới khi cây tạo ra có thể dự đoán chính xác 100% training data hoặc toàn bộ thuộc tính đã được xét tới. Tuy nhiên cách dừng thuật toán này có thể gây ra Overfiting, ở phần sau mình sẽ bàn luận chi tiết hơn. Chú ý: mỗi thuộc tính chỉ được xuất hiện một lần trên một nhánh.
Nếu bạn đã đọc bài 12. Decision Tree - ID3 (1/2) thì cách 2 độ đo information gain và gini index làm giống nhau.
Tuy nhiên, như đã đề cập ở phần đầu giới thiệu thì thuật toán CART của thư viện sklearn sẽ chỉ sử dụng một binary tree để tạo nên Decision Tree. Vậy làm sao để với một thuộc tính bao gồm nhiều hơn 2 giá trị có thể chia thành 2 child node? Ta chỉ cần xét một ngưỡng $t$ để phân tách thành giá trị thuộc tính làm 2 vùng nhỏ hơn $t$ và lớn hơn $t$. Vì vậy ở bước công thức (5), cây lúc này sẽ là cây nhị phân nên có thể viết lại như sau với thuật toán CART trong sklearn:
Một ngưỡng $t$ sẽ phân chia tập $\mathcal{S}$ thành 2 nửa: $\mathcal{S_0}$ có số lượng phần tử là $N_0$, $\mathcal{S_1}$ có số lượng phần tử là $N_1$
\[\mathbf{\text{Gini}}(x, t; \mathcal{S}) = \frac{N_0}{N}\mathbf{\text{Gini}}(x,\mathcal{S}_0) + \frac{N_1}{N} \mathbf{\text{Gini}}(x,\mathcal{S}_1)\]tới đây ta chỉ cần tuning giá trị $t$ với thuộc tính $x$ để tìm ra giá trị hàm Gini nhỏ nhất và đó chính là thuộc tính và ngưỡng mà sẽ xét làm non-leaf node. Và đây chính là hàm cost function của thuật toán CART trong bài toán phân loại.
Đọc tới đây chắc hẳn bạn đã hiểu cách một cây nhị phân được tạo ra như thế nào để fit chính xác 100% ở tập dữ liệu trên phần 2.
4. Ý nghĩa các node trong sklearn
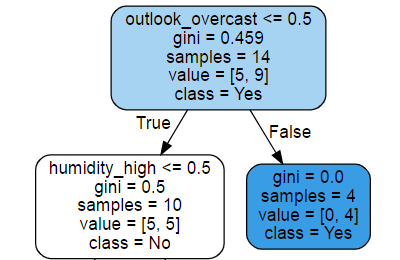
Ở node trên cùng chính là root node, các giá trị được biểu diễn như sau:
-
outlook_overcast <= 0.5: điều kiện phân tách tại node đang xét -
gini = 0.459: chỉ số gini của node tại node đang xét - công thức (4) -
samples = 14: tổng số samples tại node đang xét -
value = [5,9]: số lượng phân phối theo class (#class = 0: 5, #class = 1: 9) -
class = 1: voting class có phân phối lớn nhất làm giá trị dự đoán (nếu cần)
Nếu từ node cha rẽ sang nhánh bên phải trái là thỏa mãn điều kiện phân tách và ngược lại. Sau khi phân tách, số samples ở node cha bằng tổng samples 2 node con tạo ra. Tuy nhiên tại sao lại cần thêm 1 bước voting class khi ta dự đoán đã chính xác 100% trên tập training? Câu trả lời đơn giản rằng, nếu để một cây quyết định tạo ra tới khi hoàn toàn tinh khiết ở leaf node thì rất rất có thể xảy ra hiện tượng Overfitting. Vì vậy, cách đơn giản nhất mà ta có thể nghĩ ngay tới dừng độ sâu của cây ở một mức nào đó và sử dụng voting để đưa ra dự đoán, nhưng như vậy là chưa đủ vì vậy một số cách để giảm hiện tượng Overfitting sẽ được trình bày bên dưới.
5. Xử lí Overfiting
Nói chung trong một Decision Tree nếu cứ để cây có thể tạo ra cho tới khi toàn bộ child node trở thành leaf node sẽ xảy ra hiện tượng Overfiting. Và càng sâu thì số lượng mỗi điểm dữ liệu sẽ càng nhỏ ở mỗi non-leaf node. Dựa vào đây có 2 cách để giảm thiểu Overfitting đó là đưa ra một điều kiện dừng và cắt tỉa (Pruning).
5.1. Điều kiện dừng
Cây sẽ không tiếp tục tạo mà sẽ dừng khi gặp một số điều kiện sau:
-
Giới hạn độ sâu của cây (đã đề cập bên trên).
-
Số lượng samples của một node đạt một ngưỡng tối thiểu. Trong trường hợp này, ta chấp nhận có một số điểm bị phân lớp sai để tránh overfitting. Class cho leaf node này có thể được xác định dựa trên voting. Với phân loại nhị phân thì 30 samples là đủ tin cậy.
-
Giới hạn số lượng tất cả các loại node được tạo ra.
-
Giới hạn số lượng leaf node.
-
information gain hoặc gini index đạt một ngưỡng đủ nhỏ (không giảm hoặc giảm ít).
Trong class DecisionTreeClassifier cung cấp một số tham số với giá trị default để điều chỉnh điều kiện dừng như sau:
1
2
3
4
5
6
7
8
9
DecisionTreeClassifier(*,
criterion='gini',
max_depth=None,
min_samples_split=2,
min_samples_leaf=1,
max_features=None,
max_leaf_nodes=None,
min_impurity_decrease=0.0,
)
trong đó:
criterion='gini': Hàm đo độ tinh khiết. Có thể là gini hoặc entropymax_depth=None: Độ sâu tối đa cho một cây quyết địnhmin_samples_split=2: Số lượng samples của một node đạt một ngưỡng tối thiểumin_samples_leaf=1: Số lượng các node lá tối thiểu của cây quyết định.max_features=None: Số lượng các thuộc tính được thử và chọn ở bước tìm thuộc tính tốt nhấtmax_leaf_nodes=None: Số lượng các node lá tối đa của cây quyết định.min_impurity_decrease=0.0: Tiếp tục phân chia một node nếu như sự suy giảm của độ tinh khiết nếu phân chia lớn hơn ngưỡng này
5.2. Pruning
Trong học máy, các kĩ thuật để giảm Overfiting rất nhiều. Một kĩ thuật phổ biến đó là regularization và trong Decision Tree thì kĩ thuật này được sử dụng với cái tên Pruning (cắt tỉa). Trong Pruning, một decision tree sẽ được xây dựng tới khi mọi điểm trong training set đều được phân lớp đúng. Sau đó, các leaf node có chung một non-leaf node sẽ được xóa bỏ và biến non-leaf node trở thành một leaf-node, sau đó sử dụng phương pháp voting để chọn ra nhãn của điểm dữ liệu. Nhìn chung phương pháp này nhằm giảm size của cây được tạo ra làm giảm hiện tượng Overfitting.
PP1: Dựa vào một validation set. Trước tiên, training set được tách ra thành một cặp training set và validation set nhỏ hơn. Decision tree được xây dựng trên training set cho tới khi mọi điểm trong training set được phân lớp đúng. Sau đó, đi ngược từ các leaf node, cắt tỉa các sibling node của nó và giữ lại node bố mẹ nếu độ chính xác trên validation set được cải thiện. Khi nào độ chính xác trên validation set không được cải thiện nữa, quá trình pruning dừng lại. Phương pháp này còn được gọi là reduced error pruning.
PP2: Dựa vào toàn tạp dataset. Ở phương pháp này ta sẽ cộng thêm một thành phần điều chuẩn (regularization term) hàm Loss. Cụ thể, giả sử Decision tree cuối cùng có $K$ leaf node, tập hợp các điểm huấn luyện rơi vào mỗi leaf node lần lượt là $S_1,…,S_K$, khi đó hàm Loss sẽ là:
\[\mathcal{L} = \sum_{k = 1}^K \frac{|\mathcal{S}_k|}{N}\mathbf{\text{Gini}}(\mathcal{S}_k) + \lambda K\]trong đó $\lambda \geq 0$ và $\mathbf{\text{Gini}}(\mathcal{S}_k)$ là công thức (5). Chúng ta lựa chọn $\lambda$ là một giá trị dương tương đối nhỏ đại diện cho thành phần kiểm soát. Gía trị này lớn thể hiện vai trò của số lượng node lá tác động lên hàm chi phí lớn. Ở thời điểm ban đầu để phân loại đúng toàn bộ các quan sát thì cần số lượng node lá $K$ tương đối lớn. Sau đó chúng ta sẽ cắt tỉa dần cây quyết định sao cho mỗi một lượt cắt tỉa hàm mất mát giảm một lượng là lớn nhất. Quá trình cắt tỉa sẽ dừng cho tới khi hàm mất mát không còn tiếp tục giảm được nữa.
Trong sklearn từ phiên bản 0.22 đã cung cấp một method rất tiện ích, khá giống với cách mà PP2 làm đó là cost_complexity_pruning_path. Để hiểu hơn mình sẽ sử dụng bộ dữ liệu iris để trình bày.
- Import thư viện và xử lí data (lưu ý rằng với iris thì với chỉ 2 thuộc tính cuối cùng đã có thể phân loại tốt):
1
2
3
4
5
6
7
8
9
10
11
12
13
from sklearn.datasets import load_iris
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
import seaborn as sns
boston = load_iris()
X = boston.data[:,:-2]
y = boston.target
features = boston.feature_names[:-2]
species = boston.target_names
X_train, X_test, y_train, y_test = train_test_split(X,y,test_size = .2, random_state = 45)
- Fit và predict:
1
2
3
4
5
6
tree_clf = DecisionTreeClassifier()
tree_clf.fit(X_train,y_train)
y_train_pred = tree_clf.predict(X_train)
y_test_pred = tree_clf.predict(X_test)
print('Training accuracy: ',accuracy_score(y_train,y_train_pred))
print('Testing accuracy: ',accuracy_score(y_test,y_test_pred))
- Kết quả đúng như đúng là đã bị overfiting:
1
2
Training accuracy: 0.95
Testing accuracy: 0.6333333333333333
Vậy nếu không sử dụng điều kiện dừng thì ta còn cách nào khác mà vẫn có thể tránh Overfitting? Ta sẽ tìm cách chọn $\lambda$ tốt nhất bằng cách tìm các $\lambda$ được tạo ra trong khi train Decision Tree:
1
2
3
path = tree_clf.cost_complexity_pruning_path(X_train,y_train)
alphas = path['ccp_alphas']
print(alphas)
1
2
3
4
array([0. , 0.00277778, 0.00277778, 0.00324074, 0.00518519,
0.00555556, 0.00555556, 0.00694444, 0.00743464, 0.00868056,
0.01041667, 0.01161038, 0.01230159, 0.01581699, 0.02010944,
0.05683866, 0.06089286, 0.20756944])
Ta thấy rằng, các giá trị $\lambda$ nằm từ 0 - 0.21. Mình sẽ visualize hiệu quả của mô hình ứng với mỗi giá trị $\lambda$:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
acc_train, acc_test = [],[]
for a in alphas:
tree_clf = DecisionTreeClassifier(ccp_alpha=a)
tree_clf.fit(X_train,y_train)
y_train_pred = tree_clf.predict(X_train)
y_test_pred = tree_clf.predict(X_test)
acc_train.append(accuracy_score(y_train,y_train_pred))
acc_test.append(accuracy_score(y_test,y_test_pred))
sns.set()
plt.figure(figsize=(14,7))
sns.lineplot(y = acc_train, x = alphas, label = 'Train accuracy')
sns.lineplot(y = acc_test, x = alphas, label = 'Test accuracy')
plt.xticks(ticks = np.arange(0.00,0.25,0.01))
Kết quả:
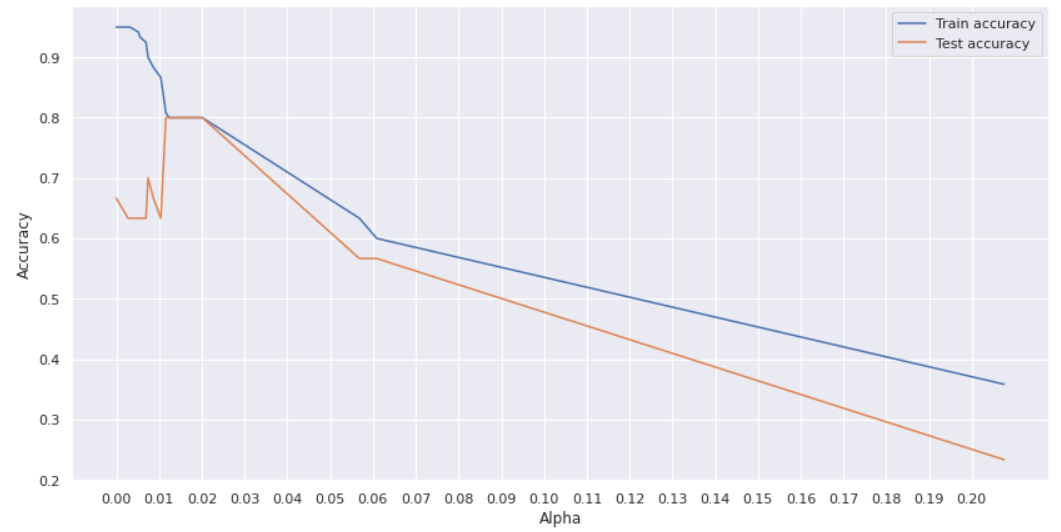
Với các giá trị $\lambda$ nằm từ 0.012 - 0.2 đưa ra giá trị accuracy của 2 tập train và test khá tương đồng nhau = 80%. Cách này cũng là một cách giảm overfitting khá tốt.
6. Regression
Một chủ đề mà mình chưa đề cập tới đó là với Decision Tree không chỉ làm việc tốt với các bài toán phân loại (classification) mà còn có thể sử dụng cho bài toán hồi quy (regression). Cụ thể với thuật toán CART mà mình đã trình bày bên trên có tên là Classification and regression tree tức thuật toán này có thể ứng dụng cho 2 lớp bài toán phân loại và hồi quy (ID3 cũng vậy). Về mặt ý tưởng thì đều dựa trên thuật toán Greedy (tham lam) để tìm ra thuộc tính phù hợp nhất và từ thuộc tính này sẽ tiếp tục phân chia tiếp. Nhưng mấu chốt ở bài toán phân loại ta cần ở mỗi node sẽ có phân phối của mỗi class còn ở bài toán hồi quy ta sẽ cần đưa ra một giá trị dự đoán cụ thể ở mỗi node, do đó thay vì sử dụng độ đo information gain hay gini cho bài toán phân loại thì ta sẽ dụng độ đo reduction in variance (độ suy giảm phương sai).
6.1. Ý tưởng
Các bước tính toán và xét ngưỡng $t$ dựa trên một thuộc tính tương tự phần 3.2 nên mình sẽ không mô tả chi tiết lại. Các bước sẽ được tóm tắt như sau:
Đầu tính phương sai của biến mục tiêu $y$ trên tập $\mathcal{S}$, đây chính là hàm Mean Square Error:
\[\text{mse}(y; \mathcal{S}) = \frac{1}{N} \sum_{i=1}^{N}(y_i-\bar{y})^2\]Tiếp theo giả sử ta chọn một thuộc tính $\mathbf{x}$ và ngưỡng $\mathbf{t}$ và phân chia tập $\mathcal{S}$ thành $\mathcal{S_0}$ có số lượng phần tử là $N_0$ và $\mathcal{S_1}$ có số lượng phần tử là $N_1$, ta sẽ tính toán tổng phương sai trên 2 tập này như sau:
\[\text{mse}(y, \mathbf{x}, \mathbf{t}; \mathcal{S}) = \frac{N_0}{N}\text{mse}(y;\mathcal{S}_0) + \frac{N_1}{N} \text{mse}(y;\mathcal{S}_1) \quad \quad (6)\]Cuối cùng giá trị $\mathbf{x}$ và ngưỡng $\mathbf{t}$ làm cho phương trình (6) nhỏ nhất sẽ được chọn. Cách này cũng khá dễ lí giải vì trong bài toán hồi quy, các dữ liệu có biến mục tiêu gần nhau thì phương sai sẽ nhỏ và ngược lại (nếu chưa từng đọc về cách hàm Mean Square Error làm như thế nào bạn có thể đọc lại bài 1 và bài 2).
6.2. Ví dụ minh họa
Sau đây là bộ dữ liệu mô tả hiệu quả của thuốc dựa trên số lượng(mg) mà một người uống, thực tế là không phải cứ uống càng nhiều thuốc càng tốt mà cần vừa đủ, với việc sử dụng Decision Tree ta sẽ tìm được kết quả là một đường khít toàn bộ dữ liệu và cây được tạo ra. Cụ thể như sau:
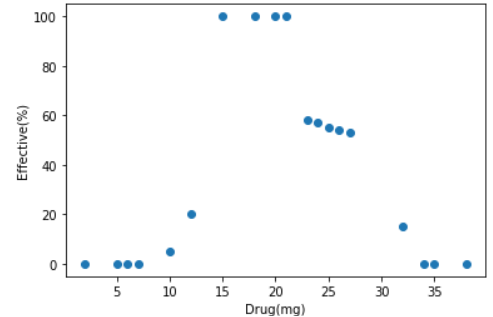
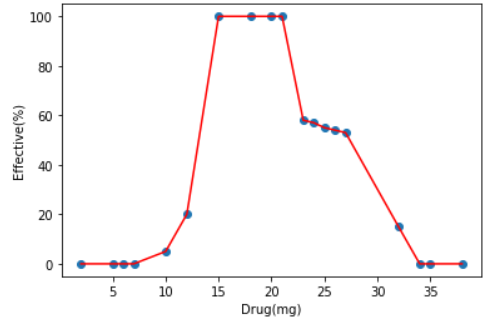
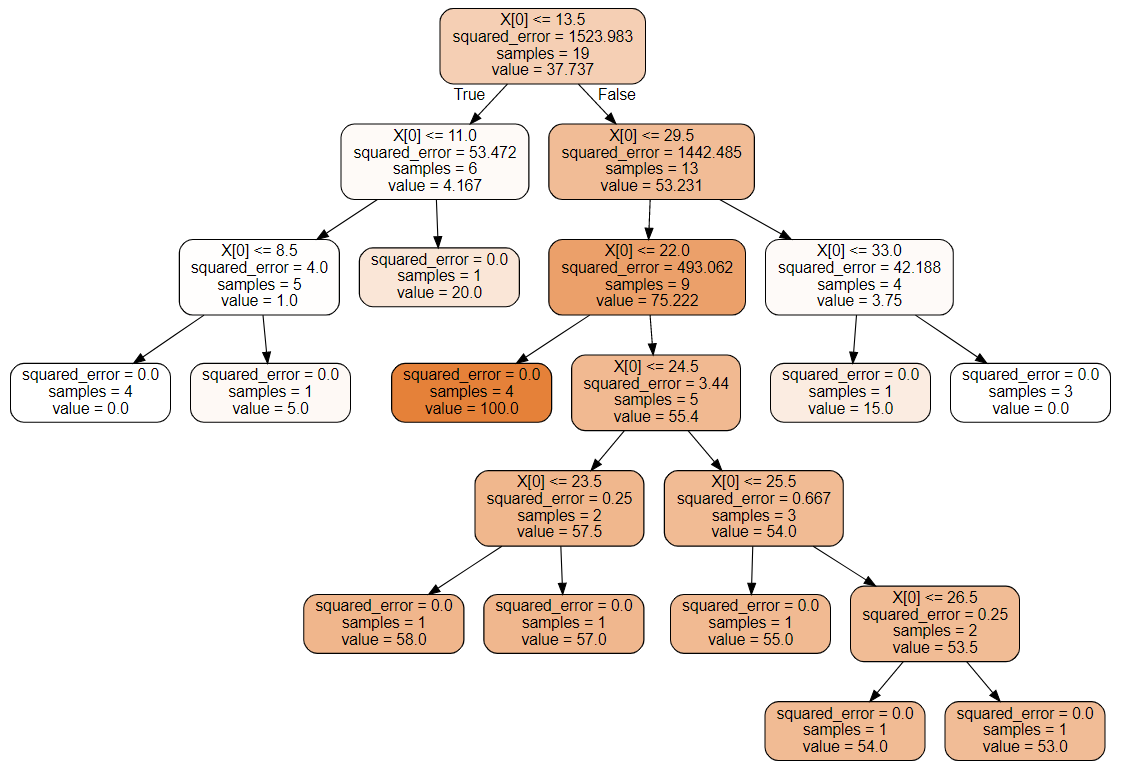
Như bạn đã thấy với dữ liệu ban đầu chỉ có duy nhất một thuộc tính, thuật toán sẽ đi tìm ngưỡng để phương trình (6) nhỏ nhất. Cụ thể ngưỡng đầu tiên ở đây là 13.5 rồi tiếp tục phân chia khi xuất hiện leaf node tức toàn bộ giá trị mse trên leaf node bằng 0. Tuy nhiên, giống với bài toán phân loại thì nếu cứ để cây có thể tạo ra cho tới khi xuất hiện đủ leaf node để dự đoán chính xác 100% trên training set thì sẽ gây ra hiện tượng Overfitting. Vì vậy các phương pháp tương tự ở phần 5 có thể áp dụng. Và giá trị dự đoán của mỗi leaf node sẽ là giá trị trung bình của những điểm dữ liệu đang xét (dòng value ở các node trên đồ thị cây).
Toàn bộ source code của bài tại đây.
7. Đánh giá và kết luận
-
Nhìn chung thì các thuật toán Decision Tree làm việc khá tốt và có thể dễ dàng debug hơn. Bởi vì nó sẽ diễn giải khá tốt những gì mà mô hình học được toàn bộ trên 1 cây, khác với các mô hình Deep Learning khá khó để hiểu chi tiết tất cả trong mô hình nó học như thế nào với các thuộc tính. Đây cũng là lí do mà người ta thường gọi rằng các thuật toán Decision Tree là white box models còn các mô hình Random Forest và Neural Netowrk là black box models.
-
Trong thuật toán Decision Tree, việc tiền xử lí như feature scaling (normalization) là không cần thiết bởi vì thuật toán sẽ đi hỏi từng thuộc tính nên việc tính toán ở mỗi thuộc tính không có ảnh hưởng tới kết quả.
-
Tuy nhiên ở các tập dữ liệu lớn đặc biệt có thuộc tính cao chiều thì sử dụng Decision Tree là một thách thức vì việc tạo cây sẽ tốn thêm rất nhiều thời gian. Không những vậy nó sẽ rất dễ gặp Overfitting trên các tập dữ liệu lớn vì các chỉ tạo ra duy nhất một cây trong khi không chỉ để giải quyết bài toán thì sẽ có nhiều cây làm được.
-
Trong cây được tạo ra, để ý rằng đôi khi có thuộc tính không xuất hiện trong cây được tạo ra nên không ảnh hưởng tới kết quả và cây được tạo ra. Để giải quyết vấn đề này bạn có thể phân tích độ tương quan dữ liệu trước khi training hoặc sau khi build cây xong sẽ có một hàm để chỉ ra mức độ quan trọng của feature (đọc thêm tại đây). Lưu ý rằng nó chỉ không được cây lựa chọn làm thuộc tính phân tách chứ không phải không có ý nghĩa phi phân tích dữ liệu.
-
Decision Tree yêu cầu khá nhiều hyper-parameters nên cách tốt nhất đó là sử dụng các phương pháp tuning để lựa chọn ra các hyper-paramters tốt nhất. Về các phương pháp tuning hyper-parameters mình sẽ trình bày một bài riêng.
-
Ngoài ra, việc sử dụng hàm entropy và gini khi training không quá khác nhau về kết quả cây được tạo ra. Tuy nhiên việc tính toán log ở entropy sẽ làm cho thuật toán chậm hơn nên ta sẽ ưu tiên sử dụng gini.
-
Hơn nữa ở các mô hình Decision Tree sẽ không ổn định (Instability). Trong sklearn thì thuật toán sẽ lựa chọn ngẫu nhiên một tập hợp các thuộc tính hữu hạn rồi đánh và và chọn để giữ tính ổn định cho mô hình bạn nên sử dụng tham số
random_state. Thêm vào đó, mô hình Decision Tree rất nhạy cảm với các biến đổi nhỏ trong training data, chỉ cần xóa một vài sample có thể dẫn tới một mô hình khác biệt hoàn toàn được tạo ra. Việc này có thể giải quyết mô hình Random Forest mà mình sẽ trình bày ở bài tiếp theo. -
Trong các cuộc thi về học máy, một trong những thành công của các thuật toán là dựa trên mô hình mạnh mẽ giúp cho việc dự đoán chính xác cao. Và các mô hình đó đều kế thừa và phát huy ý tưởng của Decision Tree, ở các bài sắp tới mình sẽ trình bày cụ thể.
8. Tham khảo
[1] Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow
[2] Bài 34: Decision Trees (1): Iterative Dichotomiser 3 - Machine Learning cơ bản by Vu Huu Tiep
[3] Decision Tree algorithm by Tuan Nguyen
[5] Regression Trees, Clearly Explained!!! by StatQuest with Josh Starmer
