Phụ lục:

• 1. Giới thiệu
• 2. Hàm Sigmoid
• 3. Hàm dự đoán
• 4. Hàm mất mát
• 5. Lập công thức chung
  • 5.1. Một điểm dữ liệu
  • 5.2. Toàn tập dữ liệu
• 6. Thực nghiệm với Python
  • 6.1. Implement thuật toán
  • 6.2. Nghiệm bằng thư viện scikit-learn
• 7. Đánh giá và kết luận
• 8. Tham khảo

1. Giới thiệu

Ở bài 1 - LinearRegression và bài 2 - Gradient Descent ta đã tìm hiểu về bài toán dự đoán (prediction) trong lớp bài toán Regression, ở bài này ta cùng tìm hiểu về bài toán phân loại (classification). Sự khác biệt cơ bản của lớp bài toán dự đoán và phân loại chính là đầu ra (output), vì giá trị dự đoán đầu ra sẽ không bị giới hạn và liên tục còn giá trị phân loại sẽ bị chặn và rời rạc. Ứng dụng của phân loại là rất nhiều trong đời sống, một số ví dụ đơn giản nhất như: phân loại nợ xấu, phân loại email spam, phân loại bệnh…

Cụ thể trong bài này ta cùng tìm hiểu về thuật toán Logistic Regression, dùng phần lớn phân loại nhị nhân (binary classification). Hiểu đơn giản phân loại nhị phân là đầu ra sẽ thuộc nhãn 0 hoặc 1. Ví dụ: nợ xấu - 1, không nợ xấu - 0; mắc ung thư - 1, không mắc ung thư - 0. Mục tiêu của phân loại nhị phân giúp dự báo xác suất xảy ra của một sự kiện, với giá trị xác suất tương ứng với nhãn 1 và nhãn 0 có tổng bằng 1. Xem hình dưới đây

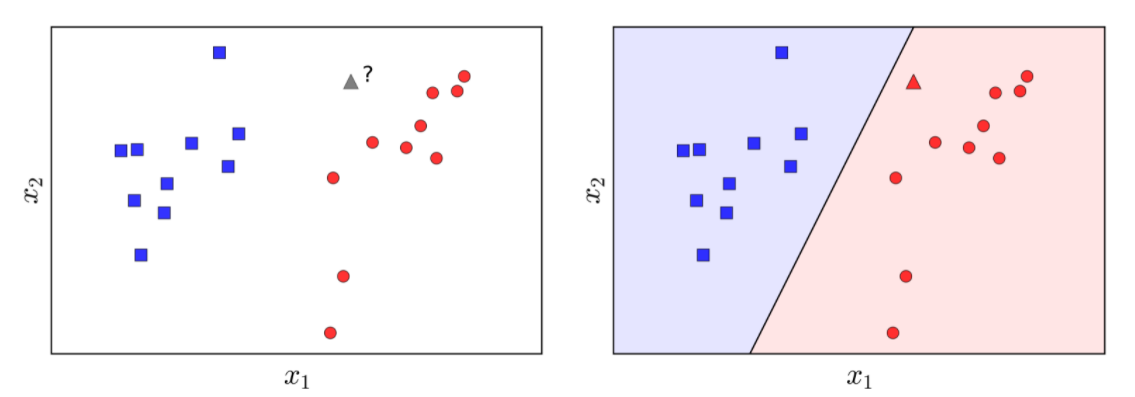
Hình 1: Bài toán nhị phân (Nguồn: machine learning cơ bản)

Ở hình trên, ta có 2 nhãn với: nhãn 1 đại diện cho các hình vuông màu xanh dương, nhãn 0 đại diện cho các hình tròn màu đỏ. Điều ta cần làm đó là dự đoán hình tam giác màu xám sẽ thuộc nhãn nào. Nhìn đơn giản ta có thể thấy, hình tam giác gần với các hình tròn màu đỏ hơn. Vì vậy ta mong xác suất mà thuộc nhãn 0 sẽ lớn hơn xác suất thuộc nhãn 1, và tổng xác suất của chúng bằng 1.

2. Hàm Sigmoid

Như đã đề cập ở trên, ta cần đầu ra là xác suất tương ứng cho mỗi nhãn. Do đó, hàm Sigmoid được ra đời để nhằm giới hạn giá trị đầu ra của bài toán Linear Regression.

Hàm Sigmoid: $f(x) = \frac{1}{1+e^{-x}}$, ta thấy đồ thị hàm Sigmoid bên dưới có giá trị giới hạn [0,1]. Thật vậy:

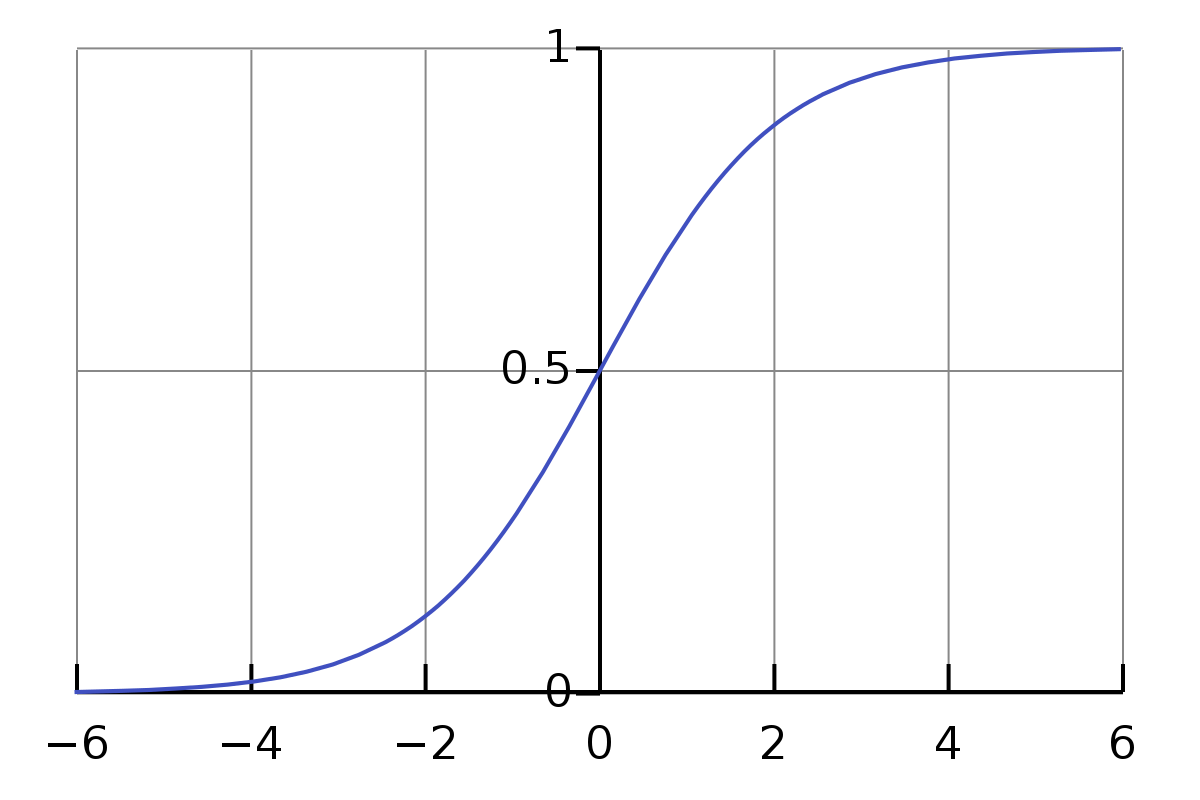
Hình 2: Đồ thị hàm Sigmoid

Ta có đạo hàm bậc nhất hàm Sigmoid như sau:

Nhận thấy rằng đạo hàm của hàm Sigmoid rất đẹp, giúp cho việc tính toán dễ dàng.

3. Hàm dự đoán

Bắt đầu với bài toán phân loại khách hàng để quyết định cho vay hoặc từ chối dựa trên mức lương và số năm kinh nghiệm. Xem hình sau

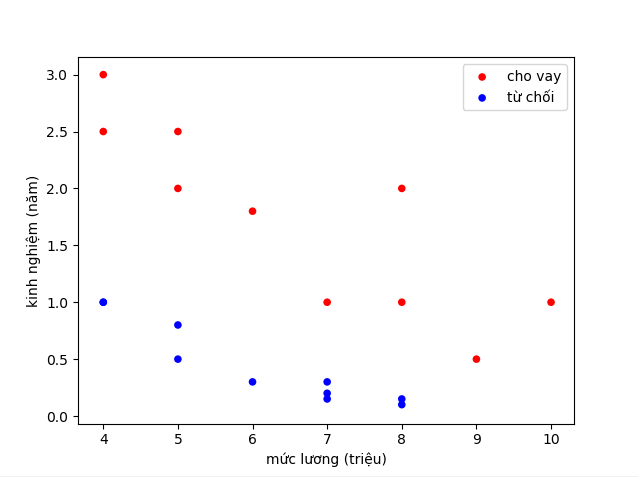
Hình 3: Visualize dữ liệu (Nguồn: deep learning cơ bản)

Ta thấy với dữ liệu như trên ta cần tìm một đường thẳng để phân chia thành 2 vùng khác nhau bao gồm: vùng cho vay - nhãn 1 màu đỏ, vùng từ chối - nhãn 0 màu xanh dương. Tuy nhiên trong bài toán phân loại, không những ta cần giá trị đầu ra mà còn muốn giá trị xác xuất của mỗi đầu ra là bao nhiêu. Ví dụ khi tiến hành mổ ung thư cho bệnh nhân, bác sĩ không muốn nói hẳn rằng ca mổ sẽ thất bại hay thành công mà thường sẽ đưa ra xác suất thành công của ca mổ cho người nhà bệnh nhân quyết định, tất nhiên xác suất càng cao sẽ càng tốt nhưng nếu chỉ là 0.5 - 0.6 thì rất cần đắn đo.

Quay lại với ví dụ trên, giả sử có một người làm việc với mức lương là $x_2$, số năm kinh nghiệm là $x_1$ thì ta sẽ có giá trị dự đoán là:

trong đó $w_0, w_1, w_2$ là các giá trị ta cần tìm và cũng là hệ số đường thẳng phân chia (boundary), $\sigma$ là kí hiệu cho hàm Sigmoid và $\hat{y}$ chính là giá trị xác suất dự đoán. Lúc này giá trị $\hat{y}$ sẽ nằm trong đoạn {0,1}. Vì vậy thường ta sẽ đặt ngưỡng là 0.5, nếu $\hat{y} >= 0.5$ ta có thể coi là nhãn 1 (vùng cho vay) và ngược lại. Biểu diễn với $c$ là viết tắt của class (nhãn):

Tất nhiên, nếu khó tính hơn thì có thể đặt ngưỡng cao hơn 0.5 để lấy được những người có thu nhập và kinh nghiệm chất lượng hơn.

4. Hàm mất mát

Hàm mất mát dược sử dụng để đo độ sai số của mô hình, tức làm cho sai số là nhỏ nhất có thể. Nếu trong dữ liệu mẫu (training set) giá trị của một sample thứ $i$ là 1 thì giá trị dự đoán $\hat{y}$ cũng cần gần 1 và tương tự với 0.

Hàm mất mát ở bài toán này sử dụng là Binary Cross Entropy, để cho dễ dàng giải thích ở đây hàm loss sẽ biểu diễn cho một điểm dữ liệu:

trong đó $y$ là giá trị 0 hoặc 1, $\hat{y}$ là giá trị dự báo nằm trong khoảng {0,1}.

Hàm loss trên, có thể chia thành 2 trường hợp:

– Nếu $y = 1 => L = -\log{(\hat{y})}$

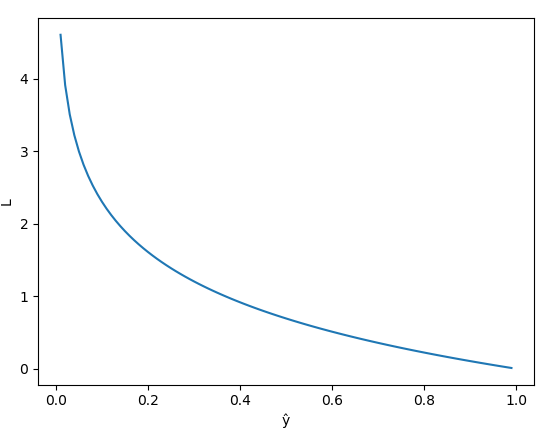
Hình 4: Visualize Loss với $y = 1$ (Nguồn: deep learning cơ bản)

Ta thấy:

• Khi giá trị của $\hat{y}$ và $y$ gần bằng nhau (tức $\hat{y}$ gần bằng 1) thì giá trị Loss sẽ giảm dần và cực gần nhau (sai số rất nhỏ) và đây cũng là điều ta mong muốn. Nhưng nếu giá trị $\hat{y}$ và $y$ khác nhau nhiều tức $\hat{y}$ tiến dần về 0 thì sai số giữa giá trị dự đoán và giá trị thực khác nhau nhiều thì giá Loss rất lớn. Điều này sẽ giúp cho mô hình làm việc hiệu quả hơn và phạt các giá trị sai tốt hơn.

– Nếu $y = 0 => L = -\log{(1 - \hat{y})}$

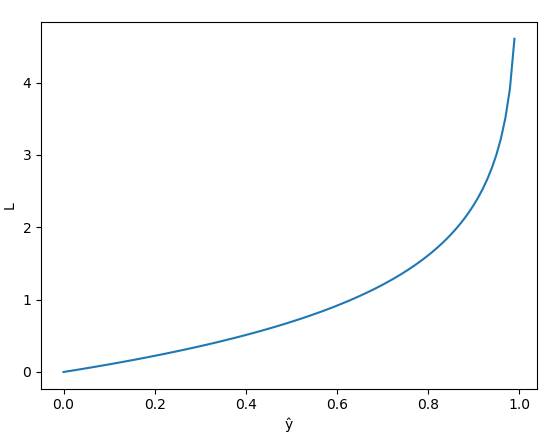
Hình 5: Visualize Loss $y = 0$ (Nguồn: deep learning cơ bản)

Ta thấy:

• Khi giá trị của $\hat{y}$ và $y$ gần bằng nhau (tức $\hat{y}$ gần bằng 0) thì giá trị Loss sẽ giảm dần. Tương tự với trường hợp $y = 1$ thì khi giá trị dự đoán và giá trị thực khác nhau nhiều thì hàm Loss sẽ có giá trị lớn.

Vì vậy, tính sai số của hàm Loss luôn được đảm bảo giữa giá trị dự đoán và giá trị thực. Hơn nữa, đồ thị luôn có cực trị tại $\hat{y} = y$.

5. Lập công thức chung

Với bài toán dự đoán cho vay hoặc từ chối nêu trên, đầu vào sẽ gồm 2 giá trị: lương và số năm kinh nghiệm. Đầu ra sẽ là xác suất tương ứng: nếu lớn hơn 0.5 thì sẽ là cho vay, nhỏ hơn 0.5 sẽ là từ chối.

5.1. Một điểm dữ liệu

Với một điểm dữ liệu thứ $i$ trong tập dữ liệu gồm $m$ mẫu, ta có:

trong đó $x_1$ và $x_2$ là giá trị lương và số năm kinh nghiệm; $w_0, w_1$ và $w_2$ là biến cần tìm; $\hat{y_i}$ là giá trị dự đoán; $\sigma$ là kí hiệu hàm Sigmoid; $y_i$ là giá trị thực.

Để tìm nghiệm cho bài toán này, ta sẽ sử dụng thuật toán Gradient Descent để tìm nghiệm (vì không thể giải và tìm nghiệm trực tiếp như bài Linear Regression).

Đặt $z_i = w_0 + w_1x_1 + w_2x_2 => \hat{y_i} = \sigma(z_i)$. Áp dụng Chain Rule ta được:

Lại có:

Từ (1),(4),(5) suy ra

Từ (2),(4),(6) suy ra

Từ (3),(4),(7) suy ra

Lúc này ta tiến hành cập nhật các nghiệm với learning rate $\alpha$:

5.2. Toàn tập dữ liệu

Cho m điểm dữ liệu và learning rate $\alpha$, ta có:

Áp dụng GD trên toàn tập dữ liệu ta được:

6. Thực nghiệm với Python

6.1. Implement thuật toán

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
import numpy as np # ĐSTT
import matplotlib.pyplot as plt # Visualize

# Hàm sigmoid
def sigmoid(x):
    return 1/(1+np.exp(-x))

# Sử dụng GD để tìm nghiệm
def process(W,X,Y,learning_rate,num_iterations):
    m = X.shape[0]
    ones = np.ones((m,1),dtype='float32')
    X = np.concatenate((ones,X),axis=1)
    cost = np.zeros((num_iterations,1))
    for i in range(num_iterations):
      y_pred = sigmoid(np.dot(X,W))
      cost[i] = -1/m*np.sum(np.multiply(Y,np.log(y_pred))+np.multiply((1-Y),np.log(1-y_pred)))
      W = W - learning_rate/m*np.dot(X.T,y_pred - Y)
    return cost,W

# Dự đoán 1 điểm dữ liệu mới
def predict(x1,x2,W,threshold):
    w0,w1,w2 = W[0][0],W[1][0],W[2][0]
    y_hat = sigmoid(w0 + w1*x1 + w2*x2)
    return 1 if y_hat >= threshold else 0

# Vẽ đường phân cách dựa trên ngưỡng
def draw_line(x21,x22,W,threshold):
    w0,w1,w2 = W[0][0],W[1][0],W[2][0]
    x11 = -(w0 + w1*x21 + np.log(1/threshold - 1))/w2
    x12 = -(w0 + w1*x22 + np.log(1/threshold - 1))/w2
    plt.plot((x21, x22),(x11,x12), 'g')
    plt.show()

def main():
    # Dữ liệu
    X = np.array([[10,5,6,7,8,9,4,5,8,4,8,7,4,5,7,4,5,6,7,8],
    [1,2,1.8,1,2,0.5,3,2.5,1,2.5,0.1,0.15,1,0.8,0.3,1,0.5,0.3,0.2,0.15]],dtype='float32').T
    
    Y = np.array([[1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0]],dtype='float32').T

    X_cho_vay = X[Y[:,0]==1] # lấy các giá trị cho vay của X
    X_tu_choi = X[Y[:,0]==0] # lấy các giá trị từ chối của X
    
    # Visualize dữ liệu
    plt.scatter(X_cho_vay[:, 0], X_cho_vay[:, 1], c='red', edgecolors='none', s=30, label='cho vay')
    plt.scatter(X_tu_choi[:, 0], X_tu_choi[:, 1], c='blue', edgecolors='none', s=30, label='từ chối')
    plt.legend(loc=1)
    plt.xlabel('mức lương (triệu)')
    plt.ylabel('kinh nghiệm (năm)')
    
    # Khởi tạo nghiêm ban đầu
    W = np.array([[0.,0.1,0.1]]).T
    
    # Khởi tạo learning rate
    learning_rate = 0.3
    
    # Khởi tạo số vòng lặp
    num_iterations = 1000
    
    # Nghiệm tìm được
    cost,W = process(W,X,Y,learning_rate,num_iterations)
    
    # Draw đường phân cách boudary dựa trên ngưỡng
    x21 = 4
    x22 = 10
    threshold = 0.5
    draw_line(x21,x22,W,threshold)
    
if __name__ == '__main__':
    main()

Kết quả:

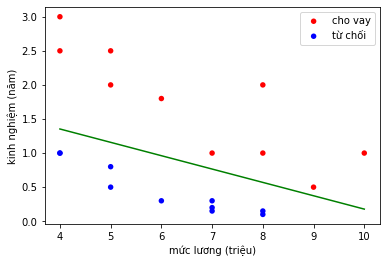
Hình 6: Kết quả cho bài toán

Chú ý: Ở hàm draw_line, ta cần dựa vào ngưỡng $\textbf{threshold}$ để vẽ được đường phân cách. Ở ví dụ đơn trên, ngưỡng $\textbf{threshold}$ được chọn là 0.5, để vẽ được đường thẳng đó ta cần 2 điểm dựa trên tọa độ.

Ta thấy với $\hat{y}$ dự đoán được, nếu $\hat{y} >= \textbf{threshold}$ tức nhãn một và cho vay tiền. Ta được:

Ở đây ta đang xét $\hat{y} \geq \textbf{threshold}$ và trục hoành lúc này là $x_2$ và trục tung là $x_1$, vậy để lấy điểm phân chia thì ta sẽ lấy dấu ‘ = ‘ $ x_2 = \frac{-(w_0 + w_1 + \ln(\frac{1}{\textbf{threshold}} - 1))}{w_2} $ và thay các giá trị $x_1$ tương ứng để lấy 2 điểm để plot Decision Boundary (đường xanh lục phía trên).

Nếu khó tính hơn, ta có thể tăng ngưỡng $\textbf{threshold}$ lên để các hợp đồng có thể vay cần có mức lương và năm kinh nghiệm cao hơn, với $\textbf{threshold} = 0.8$, lúc này 1 số người được vay lúc trước sẽ bị loại khỏi khi tăng độ khó tính bằng ngưỡng $\textbf{threshold}$

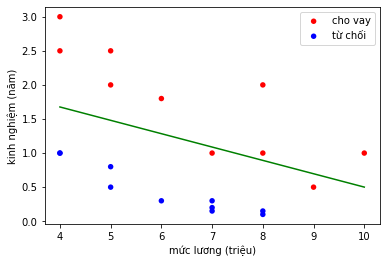
Hình 7: $\textbf{threshold} = 0.8$

Cuối cùng giá trị vector W được tìm thấy với $\text{threshold} = 0.5$

1
2
3
4
print('W = ', W)
>>> W = [[-9.1733122 ]
         [ 0.8410079 ]
         [ 4.29242685]]

6.1. Nghiệm bằng thư viện scikit-learn

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
from sklearn.linear_model import LogisticRegression
import numpy as np # ĐSTT
import matplotlib.pyplot as plt # Visualize

# Dữ liệu
X = np.array([[10,5,6,7,8,9,4,5,8,4,8,7,4,5,7,4,5,6,7,8],
[1,2,1.8,1,2,0.5,3,2.5,1,2.5,0.1,0.15,1,0.8,0.3,1,0.5,0.3,0.2,0.15]],dtype='float32').T

Y = np.array([1,1,1,1,1,1,1,1,1,1,0,0,0,0,0,0,0,0,0,0],dtype='float32')

X_cho_vay = X[Y == 1] # lấy các giá trị cho vay của X
X_tu_choi = X[Y == 0] # lấy các giá trị từ chối của X
plt.scatter(X_cho_vay[:, 0], X_cho_vay[:, 1], c='red', edgecolors='none', s=30, label='cho vay')
plt.scatter(X_tu_choi[:, 0], X_tu_choi[:, 1], c='blue', edgecolors='none', s=30, label='từ chối')
plt.legend(loc=1)
plt.xlabel('mức lương (triệu)')
plt.ylabel('kinh nghiệm (năm)')

log_reg = LogisticRegression()
log_reg.fit(X, Y)

print('b = {}, W = {}'.format(log_reg.intercept_, log_reg.coef_))

# Vẽ đường phân cách dựa trên ngưỡng
def draw_line(x21,x22,threshold):
    w0,w1,w2 = log_reg.intercept_[0], log_reg.coef_[0][0],log_reg.coef_[0][1]
    x11 = -(w0 + w1*x21 + np.log(1/threshold - 1))/w2
    x12 = -(w0 + w1*x22 + np.log(1/threshold - 1))/w2
    plt.plot((x21, x22),(x11,x12), 'g')
    plt.show()

draw_line(4,10,0.5)

Kết quả:

1
>>> b = [-6.4390718], W = [[0.66716139 2.09426755]]

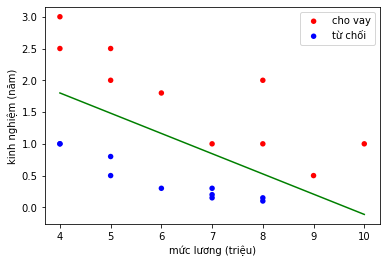
Với nghiệm của thư viện tìm được và nghiệm tự implement ở trên có chút khác biệt vì thực chất ở trong hàm có sẵn của thư viện, nhà phát triển có thể sử dụng một thuật toán tối ưu nào đó khác GD như là SGD hoặc các tham số như learning rate và số vòng lặp khác nhau sẽ đưa ra kết quả nghiệm cuối cùng khác nhau. Tuy nhiên khi plot Decision Boundary thì không có sự khác biệt quá nhiều vì đơn giản trong GD sẽ không có một nghiệm hoàn toàn chính xác 100% mà chỉ là nghiệm tối ưu, hơn nữa với hàm Loss của Logistic Regression thì vẫn đảm bảo tính Convex nên sẽ luôn đảm bảo tìm nghiệm này rất sát với Global minimum.

7. Đánh giá và kết luận

• Trong thuật toán Logistic Regression ta không thể tìm nghiệm bài toán trực tiếp như ở bài 1 - Linear Regression, vì vậy ta cần dựa trên thuật toán Gradient Descent để tìm tối ưu cho bài toán. Ở loss function của Logistic Regression, chúng ta sử dụng hàm Binary Cross Entropy vì là hàm Convex nên ta sẽ đảm bảo tìm được nghiệm tốt và có thể coi là Global minimum.

• Hàm MSE loss sẽ không phù hợp với bài toán này vì độ phạt khi 2 giá trị dự đoán và giá trị thực khau nhau nhiều sẽ không cao nên khó để kiểm soát mô hình. Nhưng quan trọng nhất là hàm MSE sẽ không Convex vì đầu ra của bài tuyến Linear sẽ cần thêm hàm activation là Sigmoid.

• Logistic Regression có thể coi là một mạng Neural Network không có hidden layer, chỉ có input layer và output layer.

• Trong thực tế, nếu dữ liệu có các dạng phân bố theo nhãn phức tạp thì Logistic Regression hoạt động không hiệu quả vì hàm dự đoán rất khó có thể tìm ra đường thẳng, mặt phẳng hoặc siêu phẳng phù hợp. Do vậy việc neural network ra đời sẽ giúp cải tiến điểm yếu này.

• Ngoài ra với Logistic Regression ta cũng có thể thực hành cho bài toán phân loại đa lớp (Multi-class classification), ý tưởng là tập hợp nhiều kết quả của bài toán nhị phân và cuối cùng đưa ra nhãn có xác suất lớn nhất từ mỗi bài nhị phân. Ví dụ với bài toán phân loại: chó, mèo, gà với input là một bức ảnh bao gồm một con vật, ta có thể chia làm 3 stage: stage 1 phân loại xem chó có xác suất bao nhiêu, stage 2 phân loại xem mèo có xác suất bao nhiêu, stage 3 phân loại xem gà có xác suất bao nhiêu. Cuối cùng sẽ lấy ra xác suất cao nhất làm nhãn (rất hiếm gần như không có trường hợp xác suất bằng nhau).

8. Tham khảo

[1] Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow

[2] Week 3 - Machine Learning coursera by Andrew Ng

[3] Bài 10: Logistic Regression - Machine Learning cơ bản by Vu Huu Tiep

[4] Bài 2: Logistic regression - Deep Learning cơ bản by Nguyen Thanh Tuan