Phụ lục:

• 1. Giới thiệu
• 2. Bài toán phân loại
  • 2.1. Ý tưởng
  • 2.2. Thực nghiệm với Python
    • 2.2.1. Implement thuật toán
    • 2.2.2. Nghiệm bằng thư viện scikit-learn
• 3. Bài toán hồi quy
  • 3.1. Ý tưởng
  • 3.2. Thực nghiệm với Python
• 4. Đánh giá và kết luận
• 5. Tham khảo

1. Giới thiệu

KNN (K-Nearest Neighbors) là một thuật toán thuộc Supervised-learning. Ý tưởng để triển khai thuật toán này rất đơn giản. Thuật toán dựa trên 2 yếu tố chính đó là: similarity measure (khoảng cách) giữa các điểm dữ liệu và nearest neighbors (“hàng xóm” lân cận) để dự đoán. Một điểm đặc biệt của thuật toán này đó là không có một hàm số giả định nào để học từ nó, khác với bài toán Linear Regression khi ta cần định nghĩa hàm số dự đoán là đường thẳng hoặc parabole. Hơn nữa, khi training thuật toán này sẽ không hề học gì từ dữ liệu, việc tính toán sẽ tập trung toàn bộ khi dự đoán một điểm dữ liệu mới.

Với những lí do nêu trên: KNN còn có thể gọi là non-parameter method, Instance-based learning, Lazy Learning, Memory-based learning. Thuật toán KNN có thể sử dụng cho 2 lớp bài toán hồi quy dự đoán (regression) và phân loại (classification) trong Supervised-leaning.

2. Bài toán phân loại

Khác với bài toán phân loại của thuật toán Logistic Regression đã được trình bày ở bài 3 - Logistic Regression sử dụng chính trong các bài toán phân loại nhị phân (binary classification), với thuật toán KNN được sử dụng để phân loại đa lớp (multi-classification). Hiểu đơn giản thì phân loại nhị phân sẽ giúp ta trả lời câu hỏi có hoặc không, ví dụ như khi phân loại email spam thì khi dự đoán một email mới đầu ra của bài toán sẽ trả lời email mới này có là email spam hay không. Nhưng với bài toán phân loại đa lớp sẽ đa dạng hơn, ví dụ khi phân loại 3 con vật chó, mèo, gà thì khi một bức ảnh mới đưa vào sẽ dự đoán nó là chó hay mèo hay gà.

2.1. Ý tưởng

Giả sử ta có tập dữ liệu như sau, 3 nhãn: 0 tương ứng hình tròn - màu đỏ, 1 tương ứng hình tam giác - màu xanh lục, 2 tương ứng hình vuông - màu xanh dương và điểm dữ liệu x - màu tím cần dự đoán thuộc nhãn nào trong 3 nhãn trên.

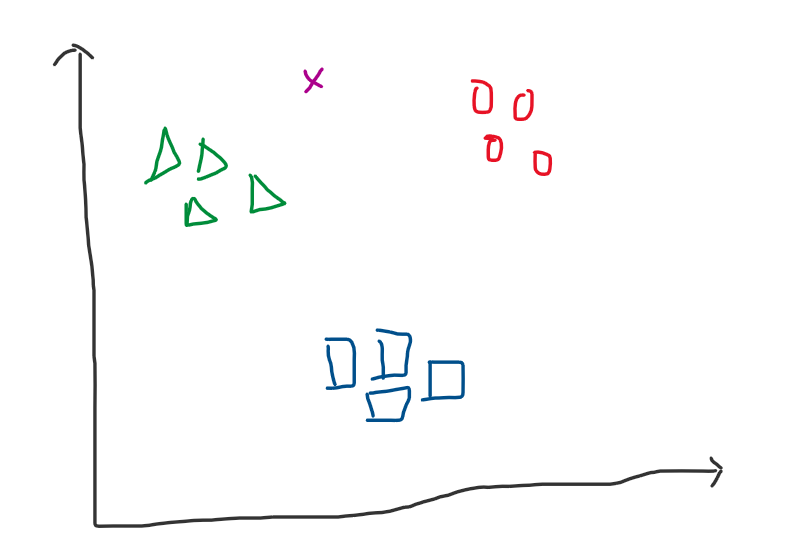
Hình 1: Dữ liệu

Ý tưởng để tìm nhãn cho dữ liệu x - màu tìm rất đơn giản.

• Bước 1: Tính toán khoảng cách giữa x với toàn bộ điểm dữ liệu

• Bước 2: Chọn ra $K$ khoảng cách ngắn nhất

• Bước 3: Với $K$ khoảng cách tìm được ở bước 2, ta sẽ xem những khoảng cách lấy ra $a$ - số lượng khoảng cách của x so với nhãn 0, tương tự $b$ - nhãn 1 và $c$ - nhãn 2. Suy ra: $a + b + c = K$.

• Bước 4: Tìm $max(a,b,c)$. Ví dụ nếu $max(a,b,c) = a$ thì dữ liệu x - màu tìm sẽ thuộc nhãn 0.

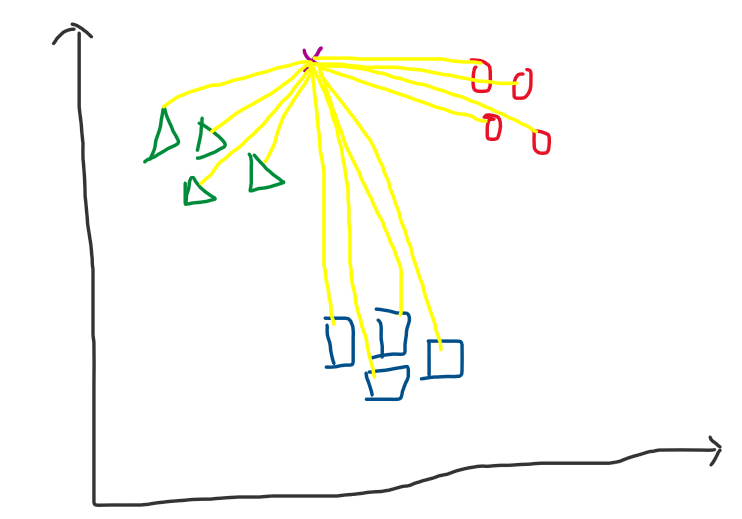
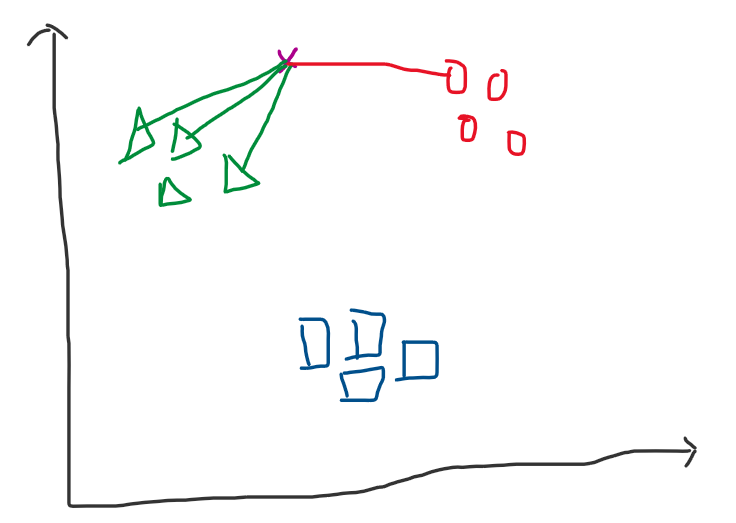
Hình 2: Bên trái - các đường thẳng màu vàng là khoảng cách giữa điểm dữ liệu x với toàn bộ dữ liệu. Bên phải chọn $K$ = 4 ta được 4 đường thẳng ngắn nhất so với x, lúc này số lượng đường thẳng so với x thuộc nhãn 1 (hình tam giác - màu xanh lục) là max. Vì vậy điểm x sẽ thuộc nhãn 1.

2.2. Thực nghiệm với Python

2.2.1. Implement thuật toán

Ở phần này, mình sẽ sử dụng một bộ thư viện có sẵn trong sklearn đó là Iris (một bộ dữ liệu về các loài hoa). Bộ dữ liệu gồm 3 nhãn: Iris setosa, Iris virginica và Iris versicolor. Mỗi nhãn có 50 bông hoa với 4 thông tin chính: chiều dài, chiều rộng đài hoa (sepal), và chiều dài, chiều rộng cánh hoa (petal). Minh họa các loài hoa trong Iris dataset:

Hình 3: Iris dataset (nguồn: Machine learning cơ bản)

Load dữ liệu

1
2
3
4
5
6
7
8
9
10
11
12
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

iris = datasets.load_iris()

X = iris.data
y = iris.target

print('Number of classes: %d' %len(np.unique(y)))
print('Number of data points: %d' %X.shape[0])
print('Features of each point: %d'%X.shape[1])

1
2
3
Number of classes: 3
Number of data points: 150
Features of each point: 4

Tiếp theo chia bộ dataset thành training set (2/3) và test set (1/3) để đánh giá hiệu năng của mô hình. Tức ta sẽ lấy kết quả ở test set làm kết quả của bài toán, ở trong bộ dữ liệu này phân phối mỗi nhãn là tương đồng nhau nên ta có thể sử dụng accuracy score để đánh giá.

1
2
3
4
5
6
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(
     X, y, test_size=50)

print("Numbers of training set: %d" %X_train.shape[0])
print("Numbers of test set: %d" %X_test.shape[0])

1
2
Numbers of training set: 100
Numbers of test set: 50

Tiếp theo ta sẽ xây dựng các hàm cần thiết cho bài toán.

• Hàm tính khoảng cách giữa 2 điểm

1
2
3
# Khoảng cách o-clit giữa 2 điểm
def distance(p1,p2):
    return np.linalg.norm(p1-p2,2)

• Hàm lấy ra toàn bộ khoảng cách với điểm xét

1
2
3
4
5
6
7
8
# Tính toàn bộ khoảng cách với điểm xét x0
def get_all_distance(x0, X, y):
    distances = []
    for i in range(len(X)):
        dist = distance(x0,X[i])
        # Lấy toàn bộ khoảng cách và nhãn tương ứng
        distances.append((dist,y[i]))
    return distance

• Hàm lấy K điểm (nhãn) gần nhất

1
2
3
4
5
6
7
8
9
# Lấy ra K điểm có khoảng cách ngắn nhất
def get_K_nearest_neighbors(K,X,y,x0):
    neighbors = []
    distances = get_all_distance(x0,X,y)
    # Sắp xếp tăng dần dựa trên khoảng cách kèm theo nhãn
    distances.sort(key=operator.itemgetter(0))
    for i in range(K):
        neighbors.append(distances[i][1])
    return neighbors

• Hàm lấy ra nhãn có lượng vote cao nhất

1
2
3
4
5
6
# Lấy ra nhãn có số vote cao nhất
def major_voting(neighbors,n_classes):
    counting = [0]*n_classes
    for i in range(n_classes):
        counting[neighbors[i]] += 1
    return np.argmax(counting)

• Hàm dự đoán và hàm tính số phần trăm chính xác

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# Hàm dự đoán
def predict(X,y,K,x0,n_classes):
    neighbors = get_K_nearest_neighbors(K,X,y,x0)
    y_pred = major_voting(neighbors,n_classes)
    return y_pred

# Tính phần trăm chính xác của dự đoán và test
def accuracy_score(y_preds,y_test):
    n = len(y_preds)
    count = 0
    for i in range(n):
        if y_preds[i] == y_test[i]:
            count += 1
    return count/n

• Hàm main

1
2
3
4
5
6
7
8
9
10
11
12
def main():
    K = 5
    n_classes = 3
    y_preds = []
    for xt in X_test:
        yt = predict(X_train, y_train, K, xt,n_classes)
        y_preds.append(yt)
    acc = accuracy_score(y_preds,y_test)
    print('Accuracy score: %f' %acc)

if __name__ == '__main__':
    main()

Kết quả:

Kết quả thu được sau vài lần chạy thường đặt được accuracy khá cao: 0.96, 0.98 thậm chí đôi khi lên tới 1.0.

1
Accuracy score: 0.980000

2.2.2. Nghiệm bằng thư viện scikit-learn

Đầu tiên ta sẽ import các thư viện cần thiết và phân chia tập train/test.

1
2
3
4
5
6
7
8
9
10
from sklearn import datasets
from sklearn.model_selection import train_test_split

iris = datasets.load_iris()

X = iris.data
y = iris.target

X_train, X_test, y_train, y_test = train_test_split(
     X, y, test_size=50)

Tiếp theo ta sẽ sử dụng class mà sklearn cung cấp để khởi tạo mô hình KNN, như đã nói ở trên thì thực chất thuật toán KNN sẽ không hề học gì từ dữ liệu vì vậy hàm fit sẽ chỉ đóng góp đưa 2 tham số X_train và y_train làm base data để dự đoán cho những dữ liệu mới.

1
2
3
from sklearn.neighbors import KNeighborsClassifier
knn_clf = KNeighborsClassifier(n_neighbors = 5, p = 2) # K = 5, norm 2 distance 
knn_clf.fit(X_train, y_train)

Sau khi khởi tạo mô hình ta sẽ dự đoán và đưa ra giá trị dự đoán trên tập test

1
2
3
4
5
y_pred = knn_clf.predict(X_test)

from sklearn.metrics import accuracy_score
acc = accuracy_score(y_test, y_pred)
print('Accuracy score: %2f' %acc)

Kết quả:

Kết quả khá tương tự với cách mình implement ở trên sẽ có sự khác nhau ở mỗi lần chạy lại thuật toán (vì mỗi lần chạy lại chia dữ liệu train/test theo một phân phối khác nhau) ,tuy nhiên thì accuracy sẽ khoảng 0.92 trở lên. Để có thể giữ độ ổn định sau mỗi lần chạy lại thuật toán ta có thể sử dụng np.random.seed(2).

1
Accuracy score: 0.960000

Có một lưu ý rằng ở kĩ thuật major_voting của thuật toán KNN là các khoảng cách K gần nhất với điểm dữ liệu đang xét có trọng số như nhau (tức độ quan trọng khoảng cách của các điểm xa điểm đang xét bằng với khoảng cách các điểm gần điểm đang xét) điều này sẽ làm mô hình KNN chưa thật sự chặt chẽ để đưa ra một đáp án cuối cùng. Vì vậy sk-learn cung cấp một attribute khi khởi tạo mô hình KNN đó là weight. Ở đoạn code trên chưa khai báo weight tức trọng số toàn bộ khoảng cách là như nhau (default là uniform), ta có thể cung cấp vào mô hình khởi tạo KNN như sau để đánh trọng số cao hơn cho khoảng cách gần hơn:

1
2
# K = 5, norm 2 distance, weights = 'distance' default: `uniform`
knn_clf = KNeighborsClassifier(n_neighbors = 5, p = 2,  weights = 'distance') 

3. Bài toán hồi quy

3.1. Ý tưởng

Ý tưởng với bài toán hồi quy cũng rất đơn giản. Giả sử ta có một tập dữ liệu như sau về thời gian học và số điểm tương ứng.

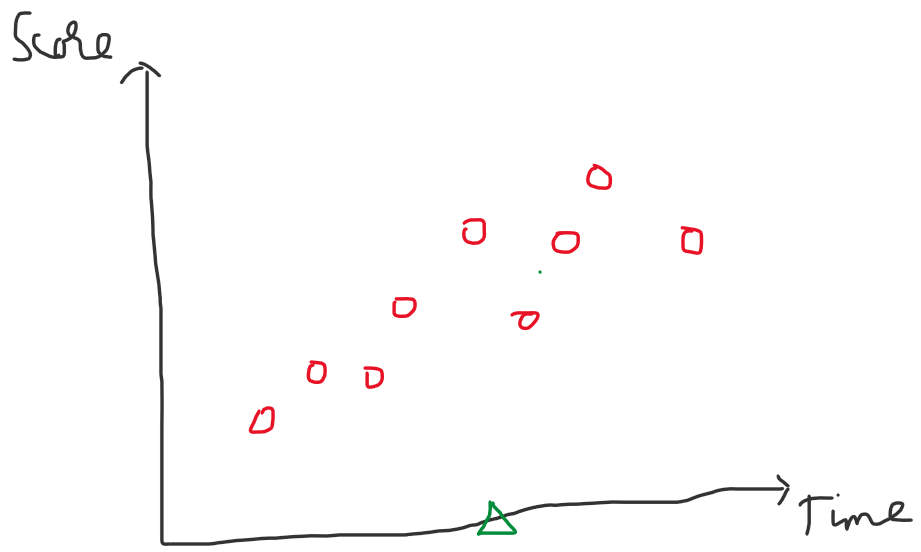
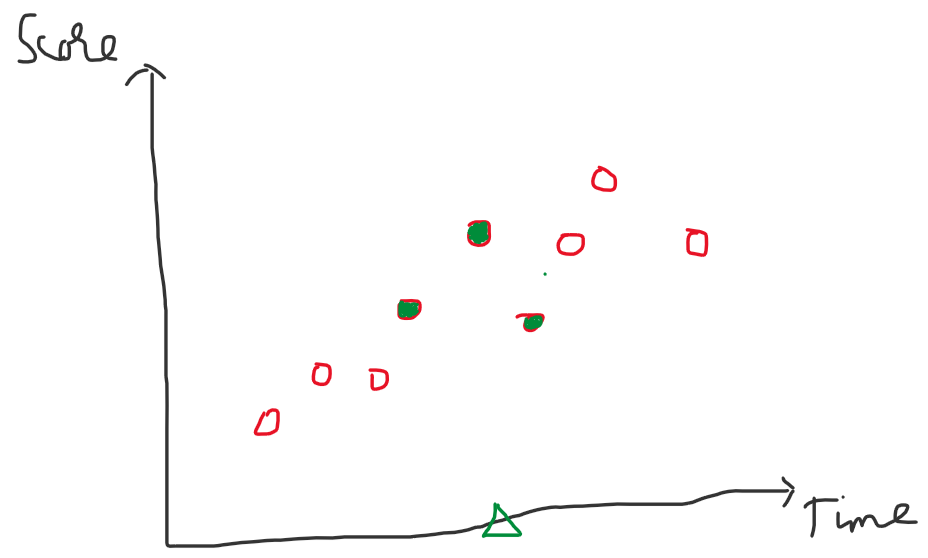
Hình 4: Dữ liệu ví dụ

Lúc này với các điểm hình tròn - màu đỏ là các dữ liệu mẫu đã có, ta cần dự đoán với điểm dữ liệu tam giác - màu xanh lục sẽ có giá trị score tương ứng là bao nhiêu với time. Ý tưởng của thuật toán KNN với bài toán hồi quy như sau:

• Bước 1: Tính khoảng cách của dữ liệu xét với toàn bộ dữ liệu mẫu.

• Bước 2: Lấy ra K dữ liệu mẫu có K khoảng cách ngắn nhất.

• Bước 3: Giá trị dự đoán là trung bình của biến mục tiêu với K dữ liệu mẫu tương ứng tìm được ở trên.

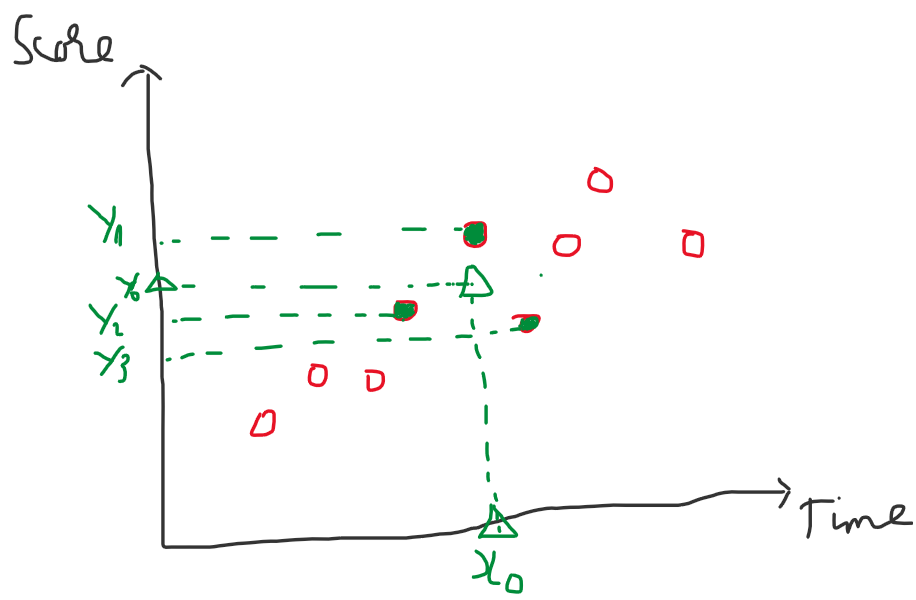
Hình 5: Bên trái - Sau khí tính toàn bộ khoảng cách, với $K$ = 3 ta lấy được 3 điểm hình tròn (lúc này màu xanh lục) là 3 giá trị có khoảng cách ngắn nhất so với điểm dữ liệu đang xét. Bên phải - Lấy trung bình các giá trị $y_1, y_2, y_3$ với 3 điểm trên ta được $y_0$ chính là giá trị cần dự đoán của $x_0$.

3.2. Thực nghiệm với Python

Vì việc code khá tương tự phần trên, nên ở phần này mình sẽ không code lại mà sử dụng thư viện sklearn và đánh giá với việc chọn $K$.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import numpy as np
import matplotlib.pyplot as plt
from sklearn import neighbors

y = np.array([[2,5,7,9,11,16,19,23,25,29,29,35,37,35,40,42,39,31,30,28,20,15,10]],dtype='float').T
X = np.array([[2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]],dtype='float').T

x0 = np.linspace(2,24,500).reshape(-1,1)
K = 3

knn = neighbors.KNeighborsClassifier(n_neighbors = K, p = 2)
knn.fit(X,y)
y_predict = knn.predict(x0)

plt.plot(x0,y_predict)
plt.plot(X,y,'ro')
plt.title('K = %d'%K)
plt.show()

Kết quả:

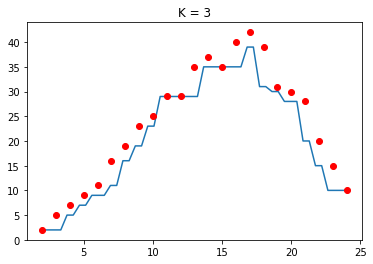
Hình 6: KNN regression

Với giá trị $K$ khác nhau ta có:

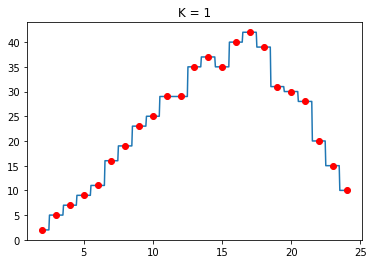
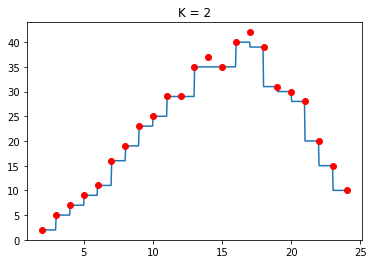
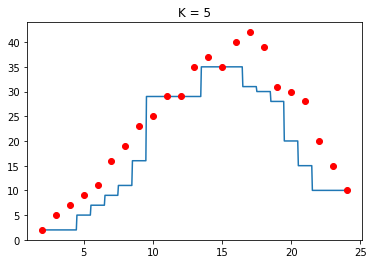
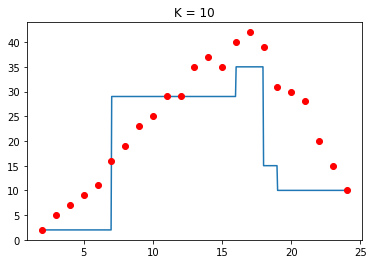
Hình 7: So sánh các giá trị $K$

Nhận xét:

• Ta thấy với giá trị $K$ nhỏ, hầu như các giá trị dự đoán rất khít với giá trị mẫu, điều này dẫn tới việc dự đoán khi có dữ liệu nhiễu (outlier) sẽ làm thuật toán bị overfitting. Vì vậy thuật toán này sẽ không thường chọn giá trị $K$ quá nhỏ. Điều này đúng với cả 2 bài toán Regression và Classification.

• Ngoài ra, trong bài toán Regression thì KNN với weight là distance sẽ làm cho điểm dự đoán có xu hướng tiến sát gần vào những điểm gần nó trong K điểm được chọn nên sẽ gây ra hiện tượng overfitting.

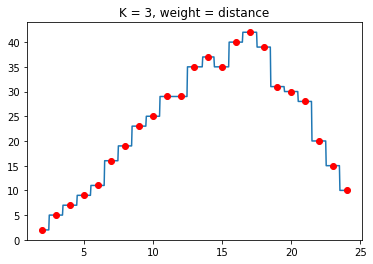
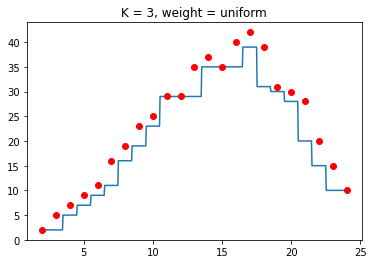
Hình 8: So sánh Weight trong Regression

Toàn bộ source code sẽ được lưu tại đây.

4. Đánh giá và kết luận

• Với thuật toán KNN thì thời gian training mô hình bằng 0 vì nó không học bất kì kiến thức gì dữ liệu. Ngược lại quá trình training và predict sẽ gom chung vào một stage nên nếu K càng lớn thì độ phức tạp của thuật toán càng cao.

• Thuật toán KNN là thuật toán đơn giản và có thể mang lại độ chính xác khá cao, nhưng khi training một tập dữ liệu lớn thì rất chậm vì việc tính toán của KNN sẽ bắt đầu lại từ đầu khi có dữ liệu mới.

• Ngoài ra trong một số trường hợp thì độ đo similarity có thể thay đổi để phù hợp hơn với dữ liệu.

5. Tham khảo

[1] Bài 6: K-nearest neighbors - Machine Learning cơ bản by Vu Huu Tiep

[2] KNN - Machine Learning and Data Mining by Khoat Than