9. Xử lí ảnh (1/2)
29 Nov 2021Phụ lục:
- 1. Giới thiệu
- 2. Mục đích của xử lí ảnh cơ bản
- 3. Không gian màu
- 4. Trục tọa độ ảnh
- 5. Tiền xử lí ảnh
- 6. Phép tích chập (Convolution)
- 7. Smoothing/Bluring
- 8. Edge detection
- 9. Kết luận
- 10. Tham khảo
1. Giới thiệu
Mục tiêu của của các bài toán xử lí ảnh là hiểu rõ những nội dung bên trong bức ảnh. Đối với mắt người, việc nhìn vào một bức ảnh để chỉ ra những đối tượng có trong bức ảnh là vô cùng dễ dàng. Nhưng đối với máy tính là một câu chuyện khác, thậm chí rất khó khăn. Tuy nhiên, các hình ảnh có khắp mọi nơi, từ các bức ảnh cá nhân từ Smartphone, Facebook, Youtube… cho tới các hình ảnh về các giấy tờ tùy thân đã được Scan lại… vì vậy việc tận dụng những nguồn dữ liệu ảnh này có rất nhiều lợi ích. Một số ứng dụng có thể kể đến, đó là:
-
Cách Facebook auto tag khi bạn xuất hiện trong một bức ảnh của người quen đăng lên.
-
Cách các thế hệ từ IphoneX có hệ thống FaceID - xác thực khuôn mặt.
-
Hay cách chuyển đổi từ chữ cái viết tay sang dạng văn bản, thậm chí ngược lại.
Có rất nhiều thư viện hỗ trợ việc xử lí ảnh trong Python nổi bật như: OpenCV, Scikit-image, Scipy, Pillow, Matplotlib… mỗi thư viện sẽ có những ưu nhược điểm riêng, nhưng nhìn chung OpenCV sẽ có nhiều điểm nổi bật hơn cả về số lượng ngôn ngữ hỗ trợ cũng như các hàm tiện ích (ultities functions) đã được dựng sẵn. Vì vậy, các bài về xử lí ảnh sẽ sử dụng OpenCV là thư viện chính để trình bày.
2. Mục đích của xử lí ảnh cơ bản
Tại thời điểm viết bài, Deep Learning đang là một xu thế rất mạnh mẽ để xử lí những bài toán về xử lí ảnh bởi dữ liệu ngày một đang được cải thiện về cả chất lượng lẫn số lượng. Tất nhiên, vai trò của xử lí ảnh ‘thuần’ sẽ bị giảm xuống và sẽ đóng góp phần lớn vào vai trò tiền xử lí nhằm giúp mô hình Deep Learning mạnh mẽ hơn. Một số tác vụ như:
-
Cải thiện chất lượng ảnh giúp con người có thể nhìn vào dễ dàng hơn, máy học tốt hơn như và ví dụ đơn giản nhất là smoothing, blurr, sharpen…
-
Chuyển đổi khung ảnh, độ phân giải giúp hiển thị trên các màn hình khác nhau vẫn giữ được tỉ lệ (aspect ratio) và độ rõ nội dung của ảnh.
-
Tăng số lượng ảnh giúp mô hình có dữ liệu phong phú hơn. Đây là một kĩ thuật rất được ưa chuộng và quan trọng các bài toán về Deep Learning khi nó cần lượng lớn dữ liệu.
-
Chuẩn hóa không gian màu phù hợp giúp máy học dễ dàng, nhanh hội tụ hơn.
-
Hoặc một số tác vụ đơn giản như thêm filter, effect lên ảnh nhằm mục đích giải trí.
Về cách máy tính đọc một bức ảnh, đọc thêm tại đây.
3. Không gian màu
Màu sắc được định nghĩa là một thuộc tính phụ thuộc tâm lí của đối tượng, vì vậy trong thực tế màu sắc của mỗi vật nhìn thấy là không giống nhau. Với những người bị mù màu vật mà họ nhìn thấy sẽ khác so với người bình thường, hoặc con người trong bóng đêm (quá tối) hoặc quá sáng sẽ không thể nhìn không rõ, nhưng sẽ có những con vật có thể nhìn rõ hơn so với bình thường. Tóm lại, màu sắc là kết quả của sự tương tác của vật và tâm lí của đối tượng nhìn vào nó.
3.1. Không gian RGB
Theo các nhà nghiên cứu về ảnh số, mắt người có cấu tạo tự nhiên rất nhạy với 3 màu Red - Gree - Blue (RBG). Vì vậy trong thực tế, các thiết bị như: Tivi, Máy ảnh, Màn hình điện thoại… đều được cấu tạo để phù hợp với mắt người và sử dụng không gian màu RGB.
Trong không gian RGB, mỗi màu được biểu diễn bởi 3 thành phần chính Red, Green, Blue. Các vector R,G,B về không gian là 3 vector trực giao với nhau. Mô hình trên hệ tọa độ Descartes:
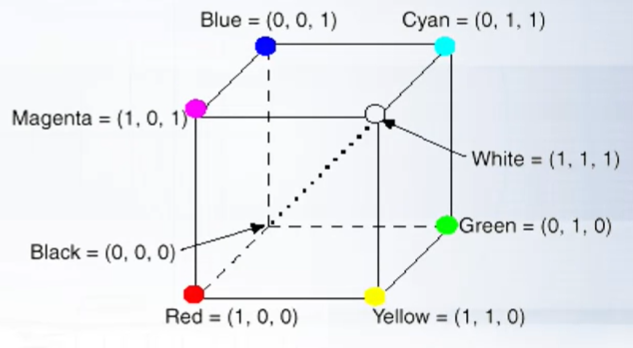
Hình 1: RGB space
Để rõ ràng hơn, hãy xem cách mỗi kênh màu Red, Green, Blue được biểu diễn:
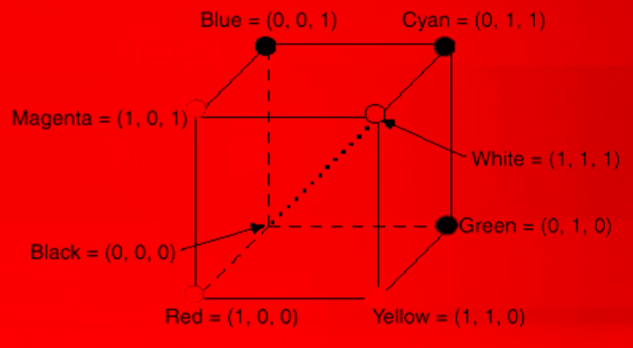
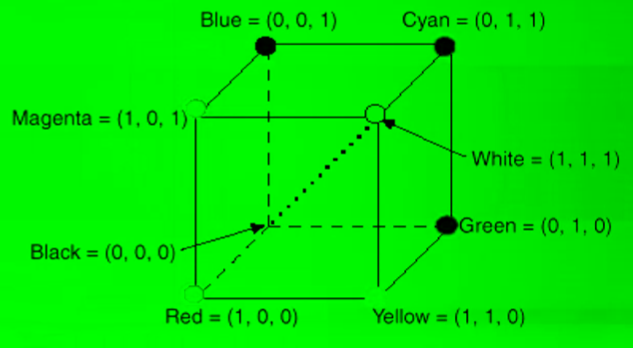
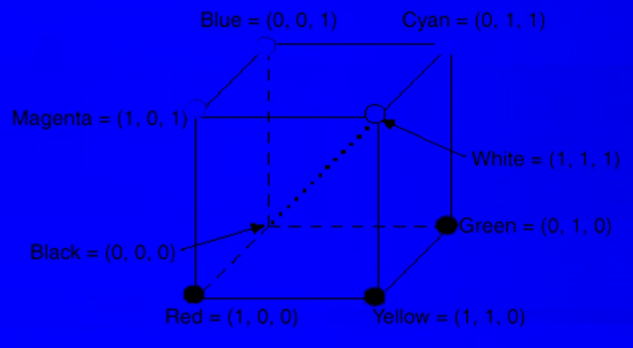
Hình 2: Red, Green, Blue channel
Tuy nhiên, hạn chế của không gian màu RGB chính là việc trộn các giá trị của ánh sáng (luminance - lighting effect) vào màu sắc thực (chrominance - pure color) trên từng channel Red, Green, Blue. Do đó việc phân tích sẽ gây khó khăn hơn vì các giá trị chưa được tách biệt, vì vậy một số không gian màu hữu ích hơn trong việc hiểu hơn nội dung ảnh được ra đời.
3.2 Không gian HSV
HSV là viết tắt của 3 từ: Hue,Saturation,Value hay còn 1 số tên gọi khác như HSI,HSB. Điểm hay của không gian HSV là có thể phân tách rõ ràng về giá trị của ánh sáng (luminance) bằng V (value) và màu sắc thực (chrominance) bằng H (Hue) + S (Saturation).

Hình 3: HSV space
-
Hue: là phần màu sắc và được biểu thị dưới dạng một số từ 0 đến 360 độ nằm trên hình nón.
-
Saturation: độ bão hòa đôi khi được xem trên phạm vi từ 0-1, trong đó 0 là màu trắng và 1 là màu chính. Ở hình 3 thì khi độ bão hòa là 0 thì màu gốc sẽ là điểm trắng - tâm hình tròn (đáy chóp).
-
Value: là ánh sáng chiếu lên đáy chóp và các màu nằm trên đáy chóp sẽ thay đổi bản chất, ta thấy ở hình 3 khi càng xuống sâu thì ánh sáng càng tối dần tức giá trị Saturation cũng giảm dần.
Vì vậy khi xử lí ảnh, nếu muốn tăng độ sáng của ảnh ta có thể xem xét làm tăng giá trị Value, nếu muốn thay đổi màu sắc ta sẽ tập trung thay đổi Hue và sử dụng Saturation để kiểm soát Hue.
3.3 Không gian YCbCr
Ngoài HSV được xử dụng phổ biến trong xử lí và phân tích, không gian YCbCr cũng được sử dụng rất phổ biến vì tính phân tách rõ ràng giá trị các vùng ánh sáng (luminance) và màu sắc thực (chrominance).
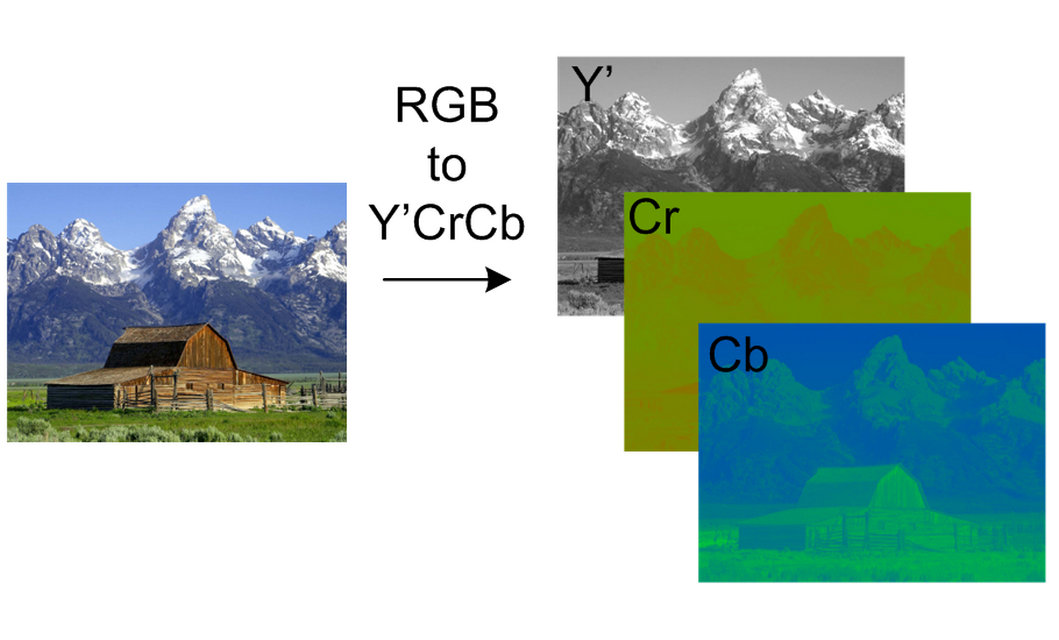
Hình 4: YCbCr space
Trong đó:
-
Y’: biểu diễn cho độ sáng (luminance), các thành phần trong không gian này bao gồm: black (low brightness) và white (high brightness)
-
Cb: Chrominance-blue và Cr: Chrominance-red. Ở phần này bao gồm: 2 không gian màu sắc (chrominance) red và blue. Hơn nữa, ở không gian YCbCr, giá trị thực màu sắc không được quan tâm một cách chính xác như giá trị Hue ở không gian HSV.
Công thức để chuyển từ RGB sang YCbCr:

Hình 5: RGB to YCbCr
3.4 Không gian Grayscale
Grayscale là một mô hình làm giảm thông tin màu bằng cách chuyển nó thành các sắc thái xám hoặc độ sáng (luminance). Mô hình này cực kỳ hữu ích để xử lý hình ảnh trong các vấn đề mà chỉ thông tin về độ sáng là đủ, chẳng hạn như nhận diện khuôn mặt. Thông thường, mỗi pixel trong hình ảnh thang độ xám được biểu thị bằng một giá trị 8 bit duy nhất, nằm trong khoảng từ 0 đối với màu đen đến 255 đối với màu trắng.

Hình 6: RGB to Grayscale
4. Trục tọa độ ảnh
Ảnh trong OpenCV được đặt gốc tọa độ (0,0) nằm phía trên cùng góc trái (upper left). Nếu đi sang phải (trục hoành) x, đi xuống (trục tung) y và giá trị của x,y đều tăng. Giả sử với một bức ảnh chữ số $\mathbf{I}$ được mô phỏng như sau:
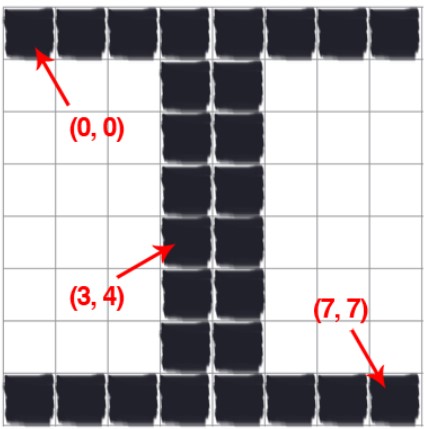
Hình 7: Chữ cái $\mathbf{I}$
Nhận xét:
-
Chúng ta thấy rằng, hình 7 bao gồm 8x8 ô và mỗi ô được hiểu là một pixel trong xử lí ảnh. Vì vậy sẽ có tổng cộng 64 pixels ở trong hình 7, chiều dài ảnh = chiều rộng = 8 (lưu ý ở đây không có khái niệm độ dài là m,mm…). Khi đọc chiều dài và chiều rộng ảnh, ta sẽ đọc hàng trước, cột sau giống như ma trận.
-
Tọa độ gốc (0,0) nằm góc trái trên cùng và tọa độ (7,7) là tọa độ góc phải dưới cùng. Toạ độ (3,4) màu đen có giá trị x = 3, y = 4 (các pixel được đánh index tương ứng như mảng 2 chiều).
-
Trong xử lí ảnh, các giá trị pixel nằm từ [0,255] và chúng ta thường dùng kiểu dữ liệu 8-bit unsigned integer để biểu diễn. Các giá trị màu càng gần 0 sẽ càng tối và càng gần 255 sẽ càng sáng.
-
Ảnh trong OpenCV được xử lí tương tự như numpy array, tức ta có thể sử dụng các toán tử với indexing - slicing để truy xuất tới 1 pixel hoặc lấy ra 1 vùng hình chữ nhật mà ta muốn.
5. Tiền xử lí ảnh
5.1. Các biến đổi hình học
Ở phần này, những kĩ thuật biến đổi từ ảnh gốc thành một số biến thể khác nhau về mặt hình học như: chuyển dịch ảnh (translation), phóng đại ảnh (scaling), xoay ảnh (rotation), lật ảnh (flipping), cắt ảnh (cropping)… Về mặt toán học bạn có thể đọc thêm tại đây.
5.1.1. Phép chuyển dịch ảnh (translation)
Chuyển dịch ảnh (translation) là một phép tịnh tiến ảnh theo hướng ngang (trục hoành) và hướng dọc (trục tung). Vì vậy, khi chuyển dịch ảnh, hình ảnh sau sẽ lên, xuống, trái, phải với bất kì phép kết hợp tịnh tiến trên. Phép dịch chuyển sẽ giữ nguyên tính chất song song của các cạnh sau dịch chuyển.
Thao tác với python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('ronaldo.jpg')
img = cv2.cvtColor(img,cv2.COLOR_BGR2RGB)
height, width, channels = img.shape
M1 = np.float32([[1, 0, 200], [0, 1, 300]])
shifted_down_right = cv2.warpAffine(img, M1, (width, height))
M2 = np.float32([[1, 0, -200], [0, 1, -300]])
shifted_up_left = cv2.warpAffine(img, M2, (width, height))
M3 = np.float32([[1, 0, 0], [0, 1, -300]])
shifted_up = cv2.warpAffine(img, M3, (width, height))
M4 = np.float32([[1, 0, -200], [0, 1, 0]])
shifted_left = cv2.warpAffine(img, M4, (width, height))
plt.figure(figsize=(16, 5))
plt.subplot(151),plt.imshow(img),plt.title('Origin Image'),plt.axis(False)
plt.subplot(152),plt.imshow(shifted_down_right),plt.title('Translate Down Right'),plt.axis(False)
plt.subplot(153),plt.imshow(shifted_up_left),plt.title('Translate Up Left'),plt.axis(False)
plt.subplot(154),plt.imshow(shifted_up),plt.title('Translate Up'),plt.axis(False)
plt.subplot(155),plt.imshow(shifted_left),plt.title('Translate Left'),plt.axis(False)
plt.show()

-
Ở phần
codetrên, các ma trậnfloat(theo yêu cầu của hàmwarpAffinetrong OpenCV) $\mathbf{M1,M2,M3,M4}$ là các ma trận chuyển dịch (translation matrix). -
Ở hàng 1 [1,0,$t_x$] có $t_x$ là số lượng pixels ảnh sẽ chuyển dịch sang trái hoặc phải. Nếu $t_x < 0$ thì ảnh sẽ dịch sang trái, $t_x > 0$ ảnh sẽ dịch sang phải, $t_x = 0$ trục ngang giữ nguyên.
-
Ở hàng 2 [0,1,$t_y$] có $t_y$ là số lượng pixels ảnh sẽ chuyển dịch lên hoặc xuống. Nếu $t_y < 0$ thì ảnh sẽ dịch lên, $t_y > 0$ ảnh sẽ dịch xuống, $t_y = 0$ trục dọc giữ nguyên.
-
Ví dụ với ma trận $\mathbf{M1}$, ảnh sẽ dịch sang phải 200 pixels, xuống 300 pixels.
5.1.2. Resize ảnh
Resize ảnh là phép biến đổi nhằm thay đổi chiều dài và chiều rộng của ảnh ban đầu. Vì vậy, tỉ lệ chiều dài và chiều rộng của ảnh cũng sẽ thay đổi. OpenCV cung cấp hàm cv2.resize bao gồm 3 đối số: src (ảnh gốc); dsize (chiều rộng mới, chiều dài mới); interpolation: là thuật toán quy định cách những pixel gần nhau được resize, gồm 5 phương pháp:
- cv2.INTER_AREA
- cv2.INTER_LINEAR
- cv2.INTER_CUBIC
- cv2.INTER_NEAREST
- cv2.INTER_CUBIC
- INTER_LANCZOS4
thường cv2.INTER_AREA cho kết quả tốt hơn trong đa số trường hợp.
1
2
3
4
5
resize_img = cv2.resize(img,(300,400),interpolation = cv2.INTER_AREA)
plt.figure(figsize=(12, 2))
plt.subplot(151),plt.imshow(img),plt.title('Origin Image'),plt.axis(False)
plt.subplot(152),plt.imshow(resize_img),plt.title('Resize '),plt.axis(False)
plt.show()

5.1.3. Phép quay ảnh (rotation)
Phép quay ảnh là một phép biến hình ảnh gốc dựa trên một góc $\theta$. Khi thực hiện một phép quay, ta cần định nghĩa chính xác điểm gốc mà mình muốn quay quanh nó, thường thì là điểm trung tâm của ảnh. Tuy nghiên, với OpenCV ta có thể chọn điểm gốc để xoay quanh nó tùy ý.
Thao tác với numpy:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
center = (width // 2, height // 2)
M1 = cv2.getRotationMatrix2D(center, 45, 1.0)
center_scale1 = cv2.warpAffine(img, M1, (width, height))
M2 = cv2.getRotationMatrix2D(center, 45, 0.5)
center_scale2 = cv2.warpAffine(img, M2, (width, height))
M3 = cv2.getRotationMatrix2D(center, 45, 2.0)
center_scale3 = cv2.warpAffine(img, M3, (width, height))
M4 = cv2.getRotationMatrix2D((0,0), 45, 1.0)
upper_left = cv2.warpAffine(img, M4, (width, height))
plt.figure(figsize=(16, 5))
plt.subplot(151),plt.imshow(img),plt.title('Origin Image'),plt.axis(False)
plt.subplot(152),plt.imshow(center_scale1),plt.title('Rotate center scale 1.0'),plt.axis(False)
plt.subplot(153),plt.imshow(center_scale2),plt.title('Rotate center scale 0.5'),plt.axis(False)
plt.subplot(154),plt.imshow(center_scale3),plt.title('Rotate center scale 2.0'),plt.axis(False)
plt.subplot(155),plt.imshow(upper_left),plt.title('Rotate upper-left scale 1.0'),plt.axis(False)
plt.show()

-
Ở phần
codetrên, các ma trận $\mathbf{M1,M2,M3,M4}$ là các ma trận chuyển dịch (translation matrix). -
Thay vì phải tự xét các giá trị bên trong ma trận chuyển dịch như phần chuyển dịch ảnh trên, OpenCV cung cấp hàm
cv2.getRotationMatrix2Dbao gồm 3 đối số:point(điểm quay),angle(góc quay),scale(hiểu đơn giản thì nó sẽ dựa vào điểmpointđã chọn để phóng đại hoặc thu nhỏ ảnh lại ví dụscale = 1.0thì độ phóng đại của ảnh vẫn giữ nguyên như ban đầu).
5.1.4. Phép lật ảnh (flipping)
Phép lật ảnh đơn giản là khi soi gương, hình ảnh mà ta nhìn thấy trong gương là một phép lật ảnh theo trục tung y. Với OpenCV ta có thể lật ảnh theo nhiều trục khác nhau như: trục tung y, trục hoành x, hoặc cả 2.
Thao tác với python:
1
2
3
4
5
6
7
8
9
10
flip_x = cv2.flip(img,1)
flip_y = cv2.flip(img,0)
flip_xy = cv2.flip(img,-1)
plt.figure(figsize=(16, 10))
plt.subplot(151),plt.imshow(img),plt.title('Origin Image'),plt.axis(False)
plt.subplot(152),plt.imshow(flip_x),plt.title('Flipping Horizontally'),plt.axis(False)
plt.subplot(153),plt.imshow(flip_y),plt.title('Flipping Vertically'),plt.axis(False)
plt.subplot(154),plt.imshow(flip_xy),plt.title('Flipping Horizontally&Vertically'),plt.axis(False)
plt.show()

- OpenCV cung cấp hàm
cv2.flipgồm 2 đối số:src(ảnh gốc),flipCode(trục lật theo, với: 1 là trục hoành, 0 là trục tung, -1 là 2 trục)
5.1.5 Cắt ảnh (cropping)
Đôi khi trong 1 bức ảnh, nhiều phần không quan trọng có thể bỏ đi. Vì vậy ta cần cắt bỏ bớt những phần đó hay nói cách khác là giữ lại phần quan tâm. Vì ảnh trong OpenCV là một numpy array, ta có thể sử dụng slicing để lấy ra những phần quan trọng nhất.
1
2
3
4
5
6
7
8
9
10
11
start_y = 100
end_y = 400
start_x = 300
end_x = 700
crop_img = img[start_y:end_y,start_x:end_x]
plt.figure(figsize=(10, 5))
plt.subplot(151),plt.imshow(img),plt.title('Origin Image'),plt.axis(False)
plt.subplot(152),plt.imshow(crop_img),plt.title('Cropped Image'),plt.axis(False)
plt.show()

5.2. Phép toán Bitwise
Phép toán Bitwise bao gồm 4 phép toán cơ bản: AND, OR, XOR, NOT. Các phép toán này tuy cơ bản nhưng khá hữu ích trong các bài về phân ngưỡng trong ảnh xám. Một pixel mang giá trị sẽ có màu đen 0 và các giá trị lớn hơn 0 sẽ có màu sáng hơn. Trước tiên xem đoạn code và 2 hình sau:
1
2
3
4
5
6
7
8
9
10
rectangle = np.zeros((300, 300), dtype = "uint8")
cv2.rectangle(rectangle, (25, 25), (275, 275), (255,0,0), -1)
circle = np.zeros((300, 300), dtype = "uint8")
cv2.circle(circle, (150, 150), 150, (255,0,0), -1)
plt.figure(figsize=(15, 2))
plt.subplot(151),plt.imshow(rectangle,cmap='gray'),plt.title('Retangle'),plt.axis(False)
plt.subplot(152),plt.imshow(circle,cmap='gray'),plt.title('Circle'),plt.axis(False)
plt.show()
Kết quả:
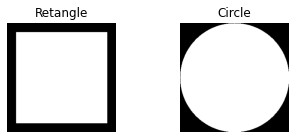
Ở đoạn code trên:
-
Dòng 1 và dòng 4 giúp vẽ 2 hình chữ nhật toàn màu đen.
-
Dòng 2 sử dụng hàm
cv2.rectangleđể vẽ hình chữ nhật màu trăng bên trong hình chữ nhật ban đầu. Các đối số trong hàmcv2.rectangle:image(ảnh vẽ),start_point(tọa độ x,y bắt đầu),end_point(tọa độ x,y kết thúc),color(màu vẽ),thickness(độ dày của nét vẽ với -1 thì sẽ vẽ bao trọn). -
Dòng 5 sử dụng hàm
cv2.circleđể vẽ hình tròn màu trắng bên trong hình chữ nhật ban đầu. Các đối số trong hàmcv2.circle:image(ảnh vẽ),center_coordinates(tọa độ tâm vẽ),radius(bánh kính),colormàu vẽ,thickness(độ dày của nét vẽ với -1 thì sẽ vẽ bao trọn).
Tiếp theo ta sẽ áp dụng các phép toán Bitwise với 2 hình trên để xem điều gì xảy ra, với đoạn code sau:
1
2
3
4
5
6
7
8
9
10
11
bitwiseAnd = cv2.bitwise_and(rectangle, circle)
bitwiseOr = cv2.bitwise_or(rectangle, circle)
bitwiseXor = cv2.bitwise_xor(rectangle, circle)
bitwiseNot = cv2.bitwise_not(circle)
plt.figure(figsize=(15, 5))
plt.subplot(151),plt.imshow(bitwiseAnd,cmap='gray'),plt.title('AND'),plt.axis(False)
plt.subplot(152),plt.imshow(bitwiseOr,cmap='gray'),plt.title('OR'),plt.axis(False)
plt.subplot(153),plt.imshow(bitwiseXor,cmap='gray'),plt.title('XOR'),plt.axis(False)
plt.subplot(154),plt.imshow(bitwiseNot,cmap='gray'),plt.title('NOT'),plt.axis(False)
plt.show()
Kết quả:
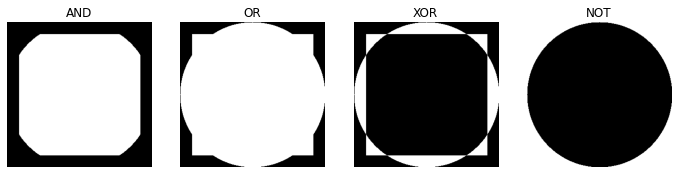
Từ đây ta có thể suy ra các quy ước về các phép toán Bitwise:
-
AND: trả về đúng khi và chỉ khi 2 pixel cùng lớn hơn 0.
-
OR: trả về đúng khi 1 trong 2 pixel lớn hơn 0.
-
XOR: trả đúng khi 1 trong 2 pixel lớn hơn 0, nhưng không phải cả 2 xảy ra.
-
NOT: đảo ngược mệnh đề.
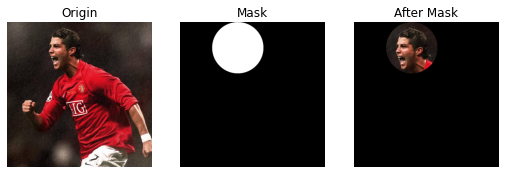
5.3. Masking
Masking là một kĩ thuật khá hay trong xử lí ảnh dựa trên toán tử Bitwise mà phần trên đã đề cập. Nó giúp chúng ta có thể tập trung vào những vùng thực sự quan tâm trong một bức ảnh. Ví dụ như bài toán nhận diện khuôn mặt (face recognition). Phần chúng ta quan tâm chỉ là khuôn mặt trong bức ảnh, những phần khác là vô nghĩa thậm chí gây khó khăn trong việc tính toán.
Với bức ảnh của Cristiano Ronaldo ở trên, ta có thể sử dụng phép toán AND để lấy ra vùng mặt bằng cách sau:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
img = cv2.imread('ronaldo.jpg')
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
mask = np.zeros(img.shape[:2],dtype='uint8')
cv2.circle(mask, (450, 200), 200, 255, -1)
masked = cv2.bitwise_and(img, img, mask = mask)
plt.figure(figsize=(15, 5))
plt.subplot(152),plt.imshow(img),plt.title('Origin'),plt.axis(False)
plt.subplot(153),plt.imshow(mask,cmap='gray'),plt.title('Mask'),plt.axis(False)
plt.subplot(154),plt.imshow(masked),plt.title('After Mask'),plt.axis(False)
plt.show()
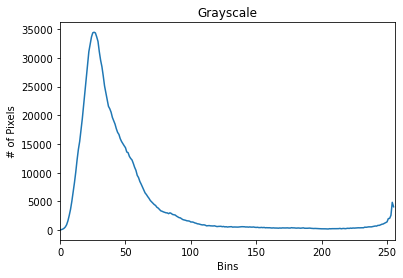
5.4. Histogram
Histogram là một khái niệm rất cơ bản trong thống kê nhằm mục đích visualize mật độ phân phối của một đối tượng. Trong xử lí ảnh, Histogram sẽ giúp chúng ta thống kê phân phối của pixel trong một bức ảnh. Nó được biểu diễn bởi một hệ tọa độ Oxy trong không gian 2D. Với trục hoành x là giá trị các pixels từ 0 - 255, trục hoành y là số lượng (tần suất) xuất hiện của mỗi pixel.
Ứng dụng của Histogram giúp chúng ta có thể hiểu được nội dung bức ảnh nhiều hơn như là: độ tương phản (contrast), độ sáng (brightness) và phân phối cường độ pixel thay vì nhìn trực tiếp vào bức ảnh.
5.4.1 Thực hành với OpenCV
OpenCV cung cấp hàm cv2.calcHist(images,channels,mask,histSize,ranges) giúp việc tính toán Histogram cho ảnh, bao gồm các đối số:
-
images: ảnh muốn tính Histogram, lưu ý khi đưa vào hàm để dạng list [image] -
channels: index list của channels ảnh, nếu muốn tính Histogram của grayscalechannels= [0]. Nếu muốn tính Histogram của Red, Green, Bluechannels= [0,1,2] -
mask: ý nghĩa củamaskgiúp tính toán với phép bitwise AND ra một Histogram. Nếu không dùng,mask= None -
histSize: số lượng bins khi tính Histogram. -
ranges: range của pixel, thường là [0,256] với ảnh Grayscal, RGB. Nếu là không gian HSV sẽ thay đổi.
Thực nghiệm với ảnh xám
1
2
3
4
5
6
7
8
9
10
11
img = cv2.imread('ronaldo.jpg')
image = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
hist = cv2.calcHist([image], [0], None, [256], [0, 256])
plt.figure()
plt.title("Grayscale")
plt.xlabel("Bins")
plt.ylabel("# of Pixels")
plt.plot(hist)
plt.xlim([0, 256])
plt.show()
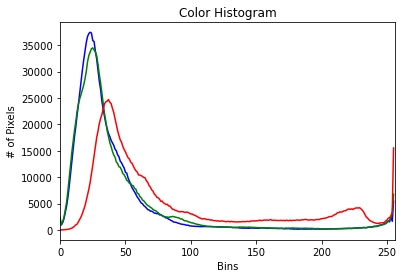
Thực nghiệm với ảnh màu
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
img = cv2.imread('ronaldo.jpg')
colors = ("b", "g", "r")
chans = cv2.split(img)
plt.figure()
plt.title("Color Histogram")
plt.xlabel("Bins")
plt.ylabel("# of Pixels")
for i in range(3):
hist = cv2.calcHist([chans[i]], [0], None, [256], [0, 256])
plt.plot(hist, color = colors[i])
plt.xlim([0, 256])
plt.show()
5.4.2 Chuẩn hóa Contrast (độ tương phản) và Brightness (ánh sáng)
Chuẩn hóa ảnh tức làm cho độ tương phản (contrast) trải đều và đa dạng. Ví dụ với bức ảnh sau:

ta thấy bức ảnh có độ tương phản không đồng đều làm cho người trong bức ảnh không nhìn rõ. Tiếp theo để hiểu rõ vấn đề hãy xem đoạn code và bức ảnh sau:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
test1 = cv2.imread('test1.jpg')
test2 = cv2.imread('test2.jpg')
im1 = cv2.cvtColor(test1, cv2.COLOR_BGR2GRAY)
im2 = cv2.cvtColor(test2, cv2.COLOR_BGR2GRAY)
hist1 = cv2.calcHist([im1], [0], None, [256], [0, 256])
hist2 = cv2.calcHist([im2], [0], None, [256], [0, 256])
fig = plt.figure(figsize=(12, 10))
fig.add_subplot(221)
plt.title('image 1')
plt.set_cmap('gray')
plt.axis('off')
plt.imshow(test1)
fig.add_subplot(222)
plt.title('histogram 1')
plt.plot(hist1)
fig.add_subplot(223)
plt.title('image 2')
plt.axis('off')
plt.set_cmap('gray')
plt.imshow(test2)
fig.add_subplot(224)
plt.title('histogram 2')
plt.plot(hist2)
plt.show()
Kết quả:
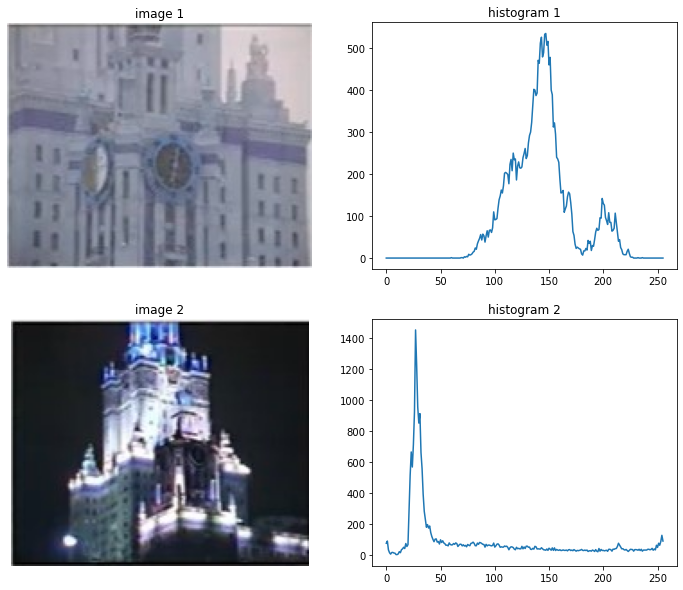
Nhận xét:
-
Ở bức ảnh 1 có biểu đồ Histogram 1 tương ứng chỉ ra một đều rằng bức ảnh không có nhiều màu đen, màu trắng và các giá trị màu sáng tối chưa được trải từ [0-255].
-
Ở bức ảnh 2 có biểu đồ Histogram 2 tương ứng chỉ ra rằng, tuy các giá trị đã nằm từ [0-255] nhưng màu đen chiếm phần rất lớn.
Một thuật toán khá phổ biến để xử lí vấn đề nêu trên là Histogram Equalization hay còn có tên gọi khác ít được sử dụng đó là Linear Histogram Normalization, ý tưởng của thuật toán này giúp phân phối màu trở nên cân bằng hơn, cải thiện độ tương phản của ảnh bằng cách trải rộng phân phối của màu.
Phương pháp này tỏ ra hữu ích khi hình ảnh chứa nền trước (foreground) và nền (background) vừa tối hoặc vừa sáng. Nó còn được sử dụng trong một số ví dụ như: nâng cao độ tương phản của hình ảnh y tế hoặc vệ tinh. Thuật toán này sẽ áp dụng trong không gian Grayscale, nơi mà các điểm sáng tối rõ ràng. Mô phỏng đầu ra của thuật toán:
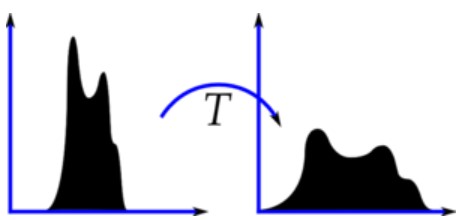
Hình 8: Histogram Equalization (Nguồn: Wiki)
OpenCV đã cung cấp một hàm cv2.equalizeHist với đối số là ảnh Grayscale. Thao tác với python:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
test = cv2.imread('check.jpg')
gray = cv2.cvtColor(test, cv2.COLOR_BGR2GRAY)
equalized_img = cv2.equalizeHist(gray)
hist_bf = cv2.calcHist([gray], [0], None, [256], [0, 256])
hist_af = cv2.calcHist([equalized_img], [0], None, [256], [0, 256])
fig = plt.figure(figsize=(12, 10))
fig.add_subplot(221)
plt.title('image before')
plt.set_cmap('gray')
plt.axis('off')
plt.imshow(gray)
fig.add_subplot(222)
plt.title('histogram before')
plt.plot(hist_bf)
fig.add_subplot(223)
plt.title('image after')
plt.axis('off')
plt.set_cmap('gray')
plt.imshow(equalized_img)
fig.add_subplot(224)
plt.title('histogram after')
plt.plot(hist_af)
plt.show()
Kết quả:
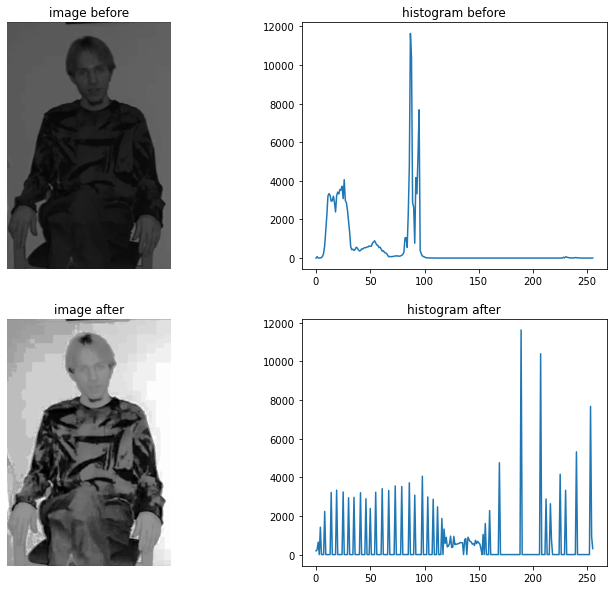
Như chúng ta đã thấy, ở bức ảnh trước khi sử dụng thuật toán Histogram Equalization các vùng sáng tối không rõ ràng. Sau khi áp dụng thuật toán này, các vùng ‘nên’ sáng như da, mặt đã được sáng rõ hơn và các đường kẻ ở áo cũng được phân tách rõ ràng hơn trước.
6. Phép tích chập (Convolution)
Convolution là khái niệm quan trọng và sử dụng nhiều nhất trong xử lý ảnh / thị giác máy tính. Convolution sẽ còn có liên quan đến các mô hình mạng học sâu (deep learning), sự phát triển của các mô hình Deep Learning hiện nay đều dựa trên kiến thức của Convolution để tạo ra các biến thể khác nhau về mô hình. Với mỗi bức ảnh, ý nghĩa của phép tích chập nhằm biến đổi thông tin đầu vào với bộ lọc để trả về đầu ra là một tín hiệu mới. Tín hiệu này sẽ làm giảm những đặc trưng mà bộ lọc không quan tâm và chỉ giữ những đặc trưng chính.
Cách hoạt động của phép tích chập (convolution) được minh họa bằng hình sau:
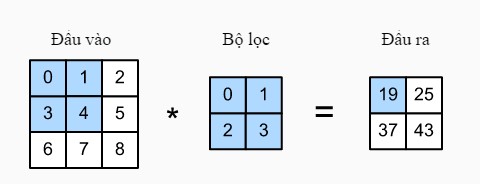
Hình 9: Convolution (Nguồn: Đắm mình vào học sâu)
Ở ảnh trên ta thấy, bắt đầu với input là một mảng 2 chiều (đầu vào) sau đó nhân tích chập với kernel (bộ lọc) theo chiều từ trái sang phải, từ trên xuống dưới và có được đầu ra tương ứng. Cụ thể như sau:
\[\begin{split}0\times0+1\times1+3\times2+4\times3=19,\\ 1\times0+2\times1+4\times2+5\times3=25,\\ 3\times0+4\times1+6\times2+7\times3=37,\\ 4\times0+5\times1+7\times2+8\times3=43.\end{split}\]Đặt chiều dài là $H$, chiều rộng là $W$ của input đầu vào; chiều dài = chiều rộng = $f$ của bộ lọc $=>$ chiều dài output = $H-f+1$, chiều rộng output = $W-f+1$. Tuy nhiên, phép tích chập chưa dừng lại ở đây, 2 khái niệm cơ bản của phép tích chập là padding và stride sẽ giúp việc giữ thông tin, giảm thông tin sau khi học từ input.
6.1. Padding
Để ma trận đầu ra có cùng chiều với ma trận đầu vào, kĩ thuật padding được ra đời. Nó sẽ mở rộng input đầu vào bằng cách thêm vector 0 vào viền làm cho sau khi nhân tích chập có chiều của output bằng với input.
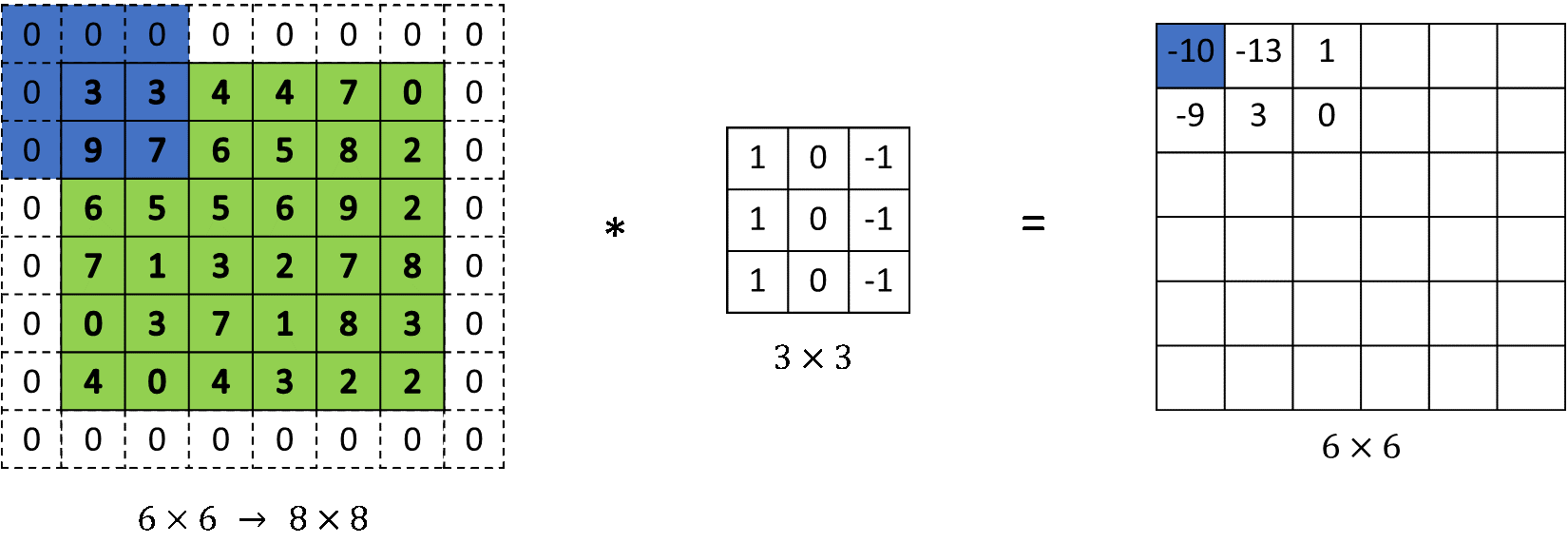
Hình 10: Padding
Giá trị $p$ để xác định số lượng vector cần thêm vào input $p = f$.
6.2. Stride
Stride là số bước nhảy khi thực hiện nhân tích chập giữa output và bộ lọc, ở hình 9 ta có stride = 1. Minh họa như sau:
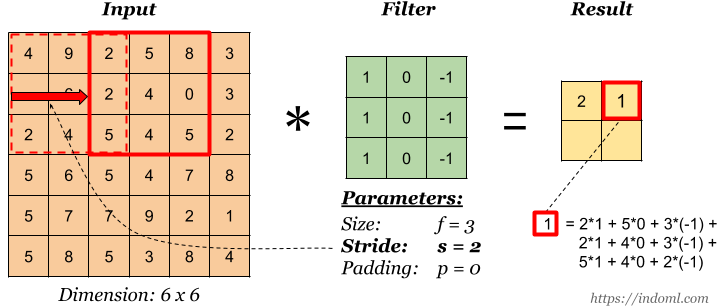
Hình 11: Stride
Từ đây ta có thể suy ra công thức tổng quát với input X $(H \times W)$, bộ lọc (kernel) $(f \times f)$, padding $p$, stride $s$ thì output sẽ có dạng như sau: $(\frac{H+2p - f}{s} + 1) * (\frac{W+2p - f}{s} + 1)$
6.3. Thực nghiệm với Python
Để ứng dụng phép toán tích chập trên, ở phần này mình sẽ code lại hàm tích chập để trích rút đặc trưng của ảnh với 2 bộ lọc:
- Bộ lọc cạnh ngang
- Bộ lọc cạnh dọc
Thao tác với python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
import cv2
import numpy as np
import matplotlib.pyplot as plt
test = cv2.imread('bridge.jpg')
gray = cv2.cvtColor(test, cv2.COLOR_BGR2GRAY)
def convolute(X, kernel, stride = 1, padding = 0):
x_h,x_w = X.shape
k_h,k_w = kernel.shape
height = (x_h + 2*padding - k_h)//stride + 1
width = (x_w + 2*padding - k_w)//stride + 1
Y = np.zeros((height,width))
for i in range(0,x_h-k_h,stride):
for j in range(0,x_w-k_w,stride):
if (i<height and j<width):
Y[i,j] = np.sum(np.multiply(X[i:i+k_h,j:j+k_w],kernel))
return Y
def normalize_range(img):
img[img > 255] = 255
img[img < 0] = 0
return img
f_x = np.array([[-1,-1,-1],
[0,0,0],
[1,1,1]])
f_y = np.array([[-1,0,1],
[-1,0,1],
[-1,0,1]])
conv_img1 = convolute(gray,f_x)
conv_img2 = convolute(gray,f_y)
conv_img1 = normalize_range(conv_img1)
conv_img2 = normalize_range(conv_img2)
imgs = [gray,conv_img1,conv_img2]
rows = 1
columns = 3
names = ['Original','Conv Vertical','Conv Horizontal']
fig = plt.figure(figsize=(30, 30))
for i in range(0,3):
fig.add_subplot(rows, columns, i+1)
plt.imshow(imgs[i],cmap='gray')
plt.axis('off')
plt.title(names[i])
plt.show()

Ta nhận thấy những bộ lọc trên có tác dụng nhận diện những đường nét theo chiều ngang, chiều dọc. Ví dụ với bộ lọc để làm nổi bật những nét chiều ngang của cây cầu đã được làm nổi bật một cách rõ ràng. Những nét chiều dọc theo bộ lọc dọc đã có thể làm nổi bật các thân cây một cách rõ ràng.
Từ đây, rất nhiều mạng nơ-rơn (neural network) kết hợp với mạng tích chập ra đời và đã tạo ra những bước đột phá trong deep learning trong lĩnh vực xử lí ảnh.
7. Smoothing/Bluring
Smoothing/Bluring là kĩ thuật rất phổ biến trong xử lí ảnh, nghĩa là làm mịn (mờ) ảnh. Trong thực tế có rất nhiều trường hợp khi ảnh chụp bị mất nét, xuất hiện các ‘răng cưa’ trên ảnh. Hiểu theo cách máy tính đọc một bức ảnh thì lúc này mỗi pixel đang bị trộn lẫn những pixel xung quanh, chúng bị trộn dính một phần vào nhau. Bước làm mịn (mờ) ảnh trước khi xử lí trực tiếp có thể giúp cải tiến chất lượng trong một số thuật toán như phân ngưỡng (thresholding), phát hiện cạnh (edge detection). Có rất nhiều phương pháp để làm mịn ảnh và sẽ có tác dụng khác nhau, chúng ta cùng xem bên dưới.
7.1. Average Bluring
Average Bluring là bộ lọc giúp làm mịn bằng cách sử dụng một cửa số trượt (sliding window) $k \times k$ đi từ trái sang phải, trên xuống dưới của bức ảnh. Trong đó, $k$ là một số số lẻ để giá trị tại tâm hình vuông $k \times k$ tồn tại. Giá trị ở giữa này sẽ là trung bình của những pixel xung quanh thuộc cửa sổ $k \times k$. Với $k$ càng lớn thì ảnh gốc sẽ được làm mờ càng nhiều.
Thao tác với python:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import cv2
import numpy as np
import matplotlib.pyplot as plt
image = cv2.imread('test.png')
small_k = cv2.blur(image, (3, 3)) # k x k = 3 x 3
medium_k = cv2.blur(image, (5, 5)) # k x k = 5 x 5
big_k = cv2.blur(image, (7, 7)) # k x k = 7 x 7
plt.figure(figsize=(16, 5))
plt.subplot(151),plt.imshow(image),plt.title('Origin Image'),plt.axis(False)
plt.subplot(152),plt.imshow(small_k),plt.title('k = 3'),plt.axis(False)
plt.subplot(153),plt.imshow(medium_k),plt.title('k = 5'),plt.axis(False)
plt.subplot(154),plt.imshow(big_k),plt.title('k = 7'),plt.axis(False)
plt.show()
Kết quả:

Nhận xét:
-
OpenCV cung cấp hàm
cv2.blurgồm 2 đối số: src (ảnh gốc) và cửa sổ trượt $k \times k$. -
Như đề đề cập bên trên thì với $k$ càng lớn sẽ làm ảnh càng mịn và loại bỏ được nhiều nhiễu hơn.
7.2. Gaussian Bluring
Gaussian Bluring khá giống với Average Bluring, nhưng thay vì lấy giá trị trung bình trên toàn bộ cửa sổ trượt như trên, ở Gaussian Bluring các giá trị pixel càng gần điểm trung bình sẽ có mức ảnh hưởng cao hơn. Đầu tiên, chúng ta cần kernel size để trượt toàn bộ bức ảnh. Sau đó, chúng ta cần xác định độ lệch chuẩn theo 2 phương X và Y là $\theta_x$ và $\theta_y$. Nếu cả 2 giá trị bằng 0, thì chúng sẽ được tính từ kernel size.
Thao tác với python:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import cv2
import numpy as np
import matplotlib.pyplot as plt
image = cv2.imread('test.png')
small_k = cv2.GaussianBlur(image, (3, 3), 0)
medium_k = cv2.GaussianBlur(image, (5, 5), 0)
big_k = cv2.GaussianBlur(image, (7, 7), 0)
plt.figure(figsize=(16, 5))
plt.subplot(151),plt.imshow(image),plt.title('Origin Image'),plt.axis(False)
plt.subplot(152),plt.imshow(small_k),plt.title('k = 3'),plt.axis(False)
plt.subplot(153),plt.imshow(medium_k),plt.title('k = 5'),plt.axis(False)
plt.subplot(154),plt.imshow(big_k),plt.title('k = 7'),plt.axis(False)
plt.show()

Nhận xét:
-
Gaussian Blur sẽ ít ảnh hưởng hơn so với Average Bluring, tuy nhiên nó sẽ giữ được tính tự nhiên của bức ảnh gốc mà trong một số trường hợp về chỉnh ảnh trong các app chụp ảnh sẽ sử dụng.
-
Phương pháp cũng được sử dụng giảm nhiễu trong ảnh khá hiệu quả.
7.3. Median Bluring
Trong phần lớn trường hợp, phương pháp Median Bluring (làm mờ trung vị) đạt hiệu quả cao nhất trung việc loại bỏ nhiễu. Giống với Average Bluring, Median Bluring cũng sẽ xác định một cửa sổ trượt $k \times k$ sau đó sẽ lấy giá trị trung vị làm giá trị trung tâm.
Thao tác với Python:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import cv2
import numpy as np
import matplotlib.pyplot as plt
image = cv2.imread('test.png')
small_k = cv2.medianBlur(image, 3)
medium_k = cv2.medianBlur(image, 5)
big_k = cv2.medianBlur(image, 7)
plt.figure(figsize=(16, 5))
plt.subplot(151),plt.imshow(image),plt.title('Origin Image'),plt.axis(False)
plt.subplot(152),plt.imshow(small_k),plt.title('k = 3'),plt.axis(False)
plt.subplot(153),plt.imshow(medium_k),plt.title('k = 5'),plt.axis(False)
plt.subplot(154),plt.imshow(big_k),plt.title('k = 7'),plt.axis(False)
plt.show()
Kết quả:

Nhận xét:
-
Có một điểm đáng chú ý ở phương pháp này đó là giá trị sau khi sử dụng bộ lọc làm mịn Median sẽ là một giá trị pixel nằm trong ảnh gốc, khác với 2 phương pháp trên là nó sẽ bị pha trộn bởi giá trị các pixel xung quanh.
-
Hiểu đơn giản thì phương pháp này sẽ loại nhiễu bằng cách bỏ đi nhiễu, còn 2 phương pháp trên loại nhiễu bằng cách pha trộn cách giá trị pixel.
7.4. Bilateral Bluring
Ở 3 phương pháp trên được sử dụng làm mờ cũng như lọc nhiễu nhưng những hình ảnh sau khi đi qua phép lọc sẽ bị mất đi các nét cạnh. Vì vậy, để có thể làm mờ mà vẫn giữ được chi tiết các nét cạnh ta sẽ tìm hiểu phương pháp bilateral blurring. Bilateral Bluring thực hiện được điều này bằng sử dụng hai phân phối Gaussian.
Hàm Gaussian thứ nhất sẽ đảm bảo rằng chỉ các pixel lân cận mới được xem xét để làm mờ, hàm Gaussian thứ 2 sẽ xem sét về sự chênh lệch cường độ đảm bảo rằng chỉ những pixel có cường độ tương tự với pixel trung tâm mới được xem xét làm mờ.
Thao tác với Python:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import cv2
import numpy as np
import matplotlib.pyplot as plt
image = cv2.imread('test.png')
small_k = cv2.bilateralFilter(image, 5, 31, 31)
medium_k = cv2.bilateralFilter(image, 7, 41, 41)
big_k = cv2.bilateralFilter(image, 9, 51,51)
plt.figure(figsize=(16, 5))
plt.subplot(151),plt.imshow(image),plt.title('Origin Image'),plt.axis(False)
plt.subplot(152),plt.imshow(small_k),plt.title('k = 5'),plt.axis(False)
plt.subplot(153),plt.imshow(medium_k),plt.title('k = 7'),plt.axis(False)
plt.subplot(154),plt.imshow(big_k),plt.title('k = 9'),plt.axis(False)
plt.show()
Kết quả:

Nhận xét:
-
OpenCV cung cấp hàm
cv2.bilateralFilterbao gồm 4 đối số lần lượt:-
src (ảnh gốc)
-
d (đường kính của mỗi vùng lân cận)
-
sigmaColor (Giá trị lớn hơn có nghĩa là nhiều màu hơn trong vùng lân cận sẽ được xem xét khi tính toán độ mờ)
-
sigmaSpace (Giá trị lớn hơn có nghĩa là các điểm ảnh ở xa điểm ảnh trung tâm hơn sẽ ảnh hưởng đến tính toán làm mờ, miễn là màu sắc của chúng đủ giống nhau)
-
-
Tuy nhiên, phương pháp này sẽ tính toán chậm hơn khá nhiều so với 3 phương pháp vì ở mỗi bước tính để làm mờ sẽ trải qua nhiều con.
8. Edge detection (phát hiện cạnh)
Trong một bức ảnh, thường tồn tại các đặc trưng như: vùng trơn, vùng nhiễu và cạnh. Cạnh trong ảnh thường mang rất nhiều thông tin hữu ích, thường sẽ là đối tượng (object) thuộc trong ảnh. Hơn nữa, ở trong các mô hình Deep Learning việc học dần dần từ cạnh rồi từ từ tới các vùng như mắt, mũi, môi (với mặt người) sẽ giúp cho đầu ra phân loại tốt hơn.
8.1. Sobel algorithm
Thuật toán Sobel là một thuật toán cổ điển nhưng khá phổ biến để phát hiện cạnh (edge detection) trong ảnh.
8.1.1. Ý tưởng thuật toán
Ý tưởng chính của thuật toán nhằm thay đổi giá trị cường độ pixel làm cho những vùng có thể chứa cạnh sẽ có giá trị thay đổi đột ngột. Đầu tiên hãy xem qua một số ví dụ sau:
Với một đường thẳng (10 x 1) trong ảnh grayscale như bên dưới, ta thấy rõ ràng rằng cường độ điểm ảnh ở giữa có sự thay đổi đột ngột và đây rất có thể là điểm cạnh của ảnh.

Tiếp theo, ta sẽ visualize biểu đồ cường độ của mỗi pixel của ảnh trên từ trái sang phải và coi rằng điểm -1 mang màu black, 1 mang màu trắng.
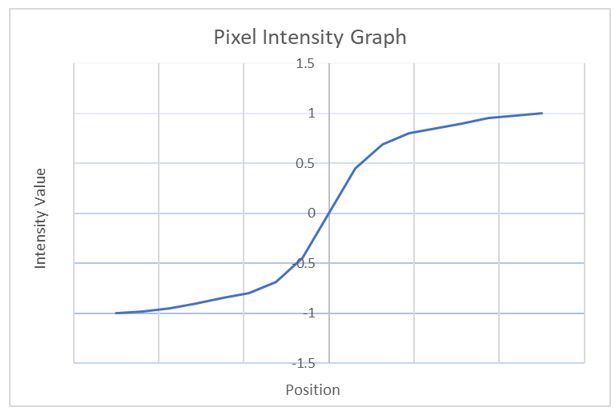
- Qua việc visualize này ta cũng có thể nhận ra rằng ở những đoạn giá trị pixel biến thiên (độ dốc) nhiều nhất gây nên sự thay đổi đột ngột và là cạnh của ảnh.
Để biết được độ biến thiên (độ dốc) của đường thẳng một cách trực quan, ta sẽ đạo hàm bậc nhất cho mỗi điểm ảnh để xem điều gì sẽ xảy ra, biểu diễn ảnh dưới đây:
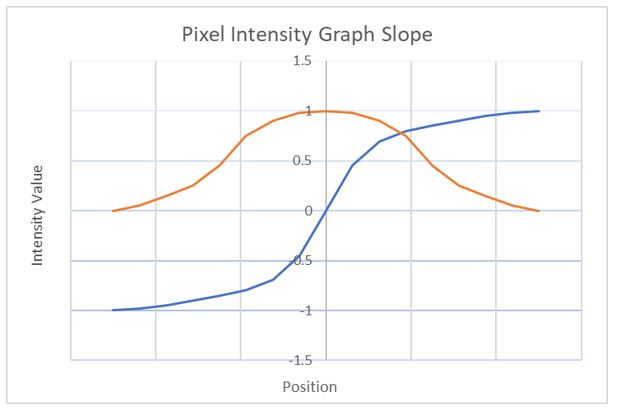
- Đường màu cam là đường biểu diễn giá trị đạo hàm tương ứng tại mỗi giá trị pixel của đường thẳng trong ảnh. Và giá trị lớn nhất đạt tại điểm giữa của đường màu cam cũng như thay đổi giá trị cường độ pixel lớn nhất. Điểm này chính là cạnh của đường thẳng ban đầu.
Từ đây ta có nhận xét rằng:
-
Gradient trong xử lí ảnh sẽ ám chỉ độ dốc về mức sáng trong ảnh.
-
Vùng ảnh trơn (smooth) thì các pixel trong vùng ảnh đó có giá trị xấp xỉ / gần bằng nhau, vì vậy khi tính toán đạo hàm sẽ gần bằng 0. Tức độ biến thiên không quá nhiều.
-
Đạo hàm dương tại một pixel thể hiện rằng biến thiên mức sáng đang ở chiều hướng đi lên, ngược lại đạo hàm âm tại một pixel cho biết biên thiên mức sáng tại đó đang giảm dần. Và ở đây sẽ gồm nhiều thông tin hữu ích như cạnh.
-
Tuy nhiên, các giá trị pixel là rời rạc nên sẽ không thể tính trực tiếp đạo hàm thay vào đó ta sẽ sử dụng phép tích chập mà ước tính được tương đương với giá trị đạo hàm.
8.1.2. Thực hành thuật toán
Các bước thực hiện:
-
B1: Thực hiện tính toán tích chập với 2 bộ lọc $f_x, f_y$ và thu được 2 bức ảnh đạo hàm theo trục tung và trục hoàn $G_x,G_y$ tương ứng.
-
B2: Tính xấp xỉ độ lớn đạo hàm bằng cách:
\[G = \sqrt{ G_{x}^{2} + G_{y}^{2} }\]- hoặc
thu được $G$ chính là ảnh đầu ra. và 2 bộ lọc $f_x,f_y$ có giá trị như sau:
\[f_x = \begin{bmatrix} -1 && 0 && 1 \\ -2 && 0 && 2 \\ -1 && 0 && 1 \end{bmatrix}\] \[f_y = \begin{bmatrix} -1 && -2 && -1 \\ 0 && 0 && 0 \\ 1 && 2 && 1 \end{bmatrix}\]Thao tác với Python
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
import cv2
import numpy as np
import matplotlib.pyplot as plt
test = cv2.imread('ronaldo.jpg')
gray = cv2.cvtColor(test, cv2.COLOR_BGR2GRAY)
def convolute(X, kernel, stride = 1, padding = 0):
x_h,x_w = X.shape
k_h,k_w = kernel.shape
height = (x_h + 2*padding - k_h)//stride + 1
width = (x_w + 2*padding - k_w)//stride + 1
Y = np.zeros((height,width))
for i in range(0,x_h-k_h,stride):
for j in range(0,x_w-k_w,stride):
if (i<height and j<width):
Y[i,j] = np.sum(np.multiply(X[i:i+k_h,j:j+k_w],kernel))
return Y
def normalize_range(img):
img[img > 255] = 255
img[img < 0] = 0
return img
def sobel(image):
f_y = np.array([[-1,-2,-1],
[0,0,0],
[1,2,1]])
f_x = np.array([[-1,0,1],
[-2,0,2],
[-1,0,1]])
img1,img2 = convolute(image,f_x,1,1),convolute(image,f_y,1,1)
img1 = normalize_range(img1)
img2 = normalize_range(img2)
square_sobel = np.sqrt(img1**2+img2**2)
abs_sobel = np.abs(img1) + np.abs(img2)
return square_sobel,abs_sobel
square_sobel,abs_sobel = sobel(gray)
fig = plt.figure(figsize=(30, 30))
rows = 1
columns = 3
imgs = [gray,square_sobel,abs_sobel]
names = ['original','square_sobel','abs_sobel']
for i in range(0,3):
fig.add_subplot(rows, columns, i+1)
plt.imshow(imgs[i],cmap='gray')
plt.axis('off')
plt.title(names[i])

8.2. Canny algorithm
Ở trên chúng ta đã tìm hiểu thuật toán Sobel trong phát hiện cạnh, tuy nhiên có một thuật toán sẽ giúp việc phát hiện cạnh chính xác cao hơn, đó là thuật toán Canny - một thuật toán phổ biến nhất trong phát hiện cạnh.
8.2.1. Các bước thực hiện
Thuật toán Canny là thuật toán bao gồm nhiều bước và ở mỗi bước nó sẽ có mục tiêu khác nhau. Các bước bao gồm:
B1: Giảm nhiễu ảnh bằng GaussianBlur (thông thường kernel có size bằng 5 x 5 sẽ hoạt động tốt, tất nhiên bạn có thể thử tăng hoặc giảm size này).
B2: Tính Gradient và hướng gradient. Đầu tiên ta sẽ sử dụng 2 bộ lọc Sobel X và Sobel Y đã được chỉ ra ở phần trên để tính toán xấp xỉ đạo hàm ảnh và thu được 2 ma trận $G_x$ và $G_y$. Tiếp theo ta sẽ tính toán
- Độ lớn Gradient theo công thức: mỗi pixel trên ma trận này thể hiện độ lớn của biến đổi mức sáng ở vị trí tương ứng trên ảnh gốc
- Hướng Gradient: mỗi pixel trên ma trận này thể hiện góc, hay nói cách khác là hướng của cạnh trên ảnh gốc.
B3: Non-Maximum Suppression. Ở bước này nhằm lọc những pixel mà có thể là điểm của cạnh cao nhất. Ta sẽ dùng filter 3x3 lần lượt chạy qua các pixel trên ảnh gradient. Trong quá trình lọc, ta xem xét xem độ lớn gradient của pixel trung tâm có phải là cực đại (lớn nhất trong cục bộ - local maximum) so với các gradient ở các pixel xung quanh. Nếu là cực đại, ta sẽ giữ pixel đó lại. Còn nếu không phải, ta sẽ set độ lớn gradient của nó về 0. Để làm điều đó, ta sẽ chỉ so sánh pixel trung tâm theo hướng gradient với góc 0, 45, 90, 135 độ. Hãy xem ví dụ biểu diễn sau:
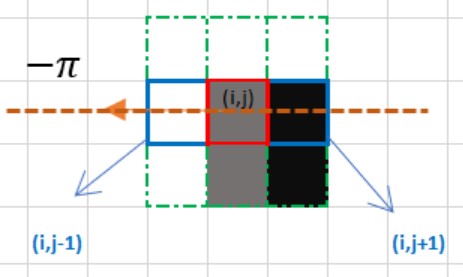
Với bức ảnh trên, hướng gradient của cạnh tại điểm (i,j - ô màu đỏ) có màu nâu nét đứt có hướng từ phải sang trái, vì vậy ta sẽ so sánh giá trị với 2 ô (i,j-1) và (i,j+1). Ở đây ta thấy điểm (i,j-1) có giá trị cao nhất và lớn ô (i,j) đang xét, vì vậy ta sẽ thay đổi giá trị ô (i,j) này thành 0. Kết thúc bước này ta sẽ thu được một ảnh nhị phân (binary image).
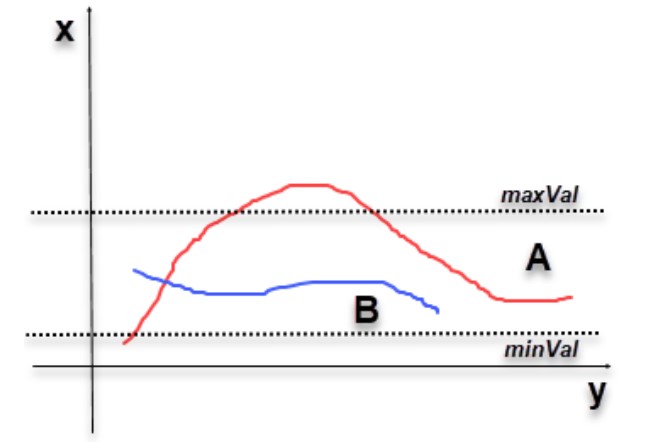
B4: Lọc ngưỡng. Ở bước này ta sẽ xét 2 ngưỡng là minVal, maxVal và mục tiêu ta sẽ phân ra được 3 loại pixels có cường độ: mạnh, yếu, không liên quan.
-
Những pixels có giá trị càng lớn thì càng có thể là cạnh của ảnh vì vậy ta sẽ sử dụng maxVal để tìm ra những pixels cường độ mạnh.
-
Những pixels yếu là những pixels có giá trị nhỏ hơn maxVal và lớn hơn minVal, ở đây có thể được xem xét thêm 1 bước nữa để xác định loại bỏ hay giữ lại vì có thể giá trị này rất sát với những pixels có thể là cạnh.
-
Những pixels không liên quan là pixels mà giá trị nhỏ hơn minVal ta sẽ loại bỏ.
Ví dụ minh họa:
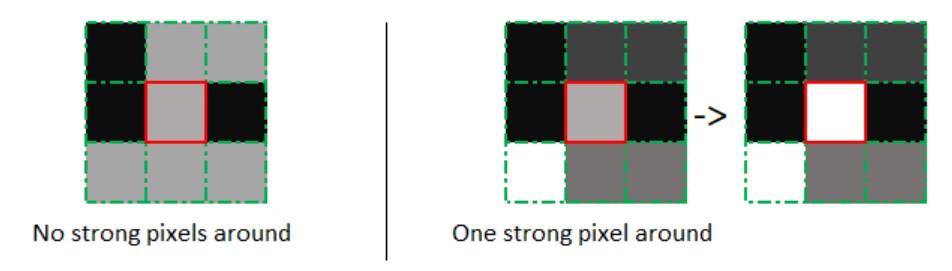
B5: Xác định cạnh qua độ trễ. Như đã đề cập ở bước 4, một pixels được coi là yếu có thể được xem xét là cạnh khi và chỉ xung quanh pixel ấy (tức pixel đang xét là tâm của hình vuông 3 x 3) có một pixel có cường độ mạnh (cạnh). Hình ảnh minh họa:
8.2.2. Thực nghiệm với Python
- Load ảnh và chuyển sang gray image

- Hàm convolution đã implement ở trên
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def convolute(X, kernel, stride = 1, padding = 0):
"""
Parameters
----------
X : Input image
kernel : kernel matri
Returns
-------
Y : Convoluted image
"""
x_h,x_w = X.shape
k_h,k_w = kernel.shape
height = (x_h + 2*padding - k_h)//stride + 1
width = (x_w + 2*padding - k_w)//stride + 1
Y = np.zeros((height,width))
for i in range(0,x_h-k_h,stride):
for j in range(0,x_w-k_w,stride):
if (i<height and j<width):
Y[i,j] = np.sum(np.multiply(X[i:i+k_h,j:j+k_w],kernel))
return Y
- Ở phần trên ta đã sử dụng hàm
cv2.GaussianBlurđể thực hiện phép làm mờ ảnh, ở phần này mình sẽ trình bày cách implement. Khởi tạo gassian kernel với công thức
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def gaussian_kernel(kernel_size, sigma=1):
"""
Parameters
----------
kernel_size : odd number
sigma : standard deviation
Returns
-------
g : kernel matrix (sliding window)
"""
size = int(kernel_size) // 2
x, y = np.mgrid[-size:size+1, -size:size+1]
normal = 1 / (2.0 * np.pi * sigma**2)
g = np.exp(-((x**2 + y**2) / (2.0*sigma**2))) * normal
return g
Kết quả khi thực hiện hàm Gaussian Blur

- Tiếp theo ta sẽ xử lí hàm tìm Gradient và hướng của ảnh
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def sobel(image):
"""
Parameters
----------
image : Blured image
Returns
-------
G : Gradient image
theta : Angle image (radian type)
"""
f_y = np.array([[-1,-2,-1],
[0,0,0],
[1,2,1]])
f_x = np.array([[-1,0,1],
[-2,0,2],
[-1,0,1]])
G_x,G_y = convolute(image,f_x,1,1),convolute(image,f_y,1,1)
G = np.hypot(G_x,G_y) # sqrt(G_x**2 + G_y**2)
G = G / G.max() * 255 # normalize range
theta = np.arctan2(G_y, G_x)
return G,theta
Kết quả của hàm sobel tìm ra được ảnh Gradient và Angle
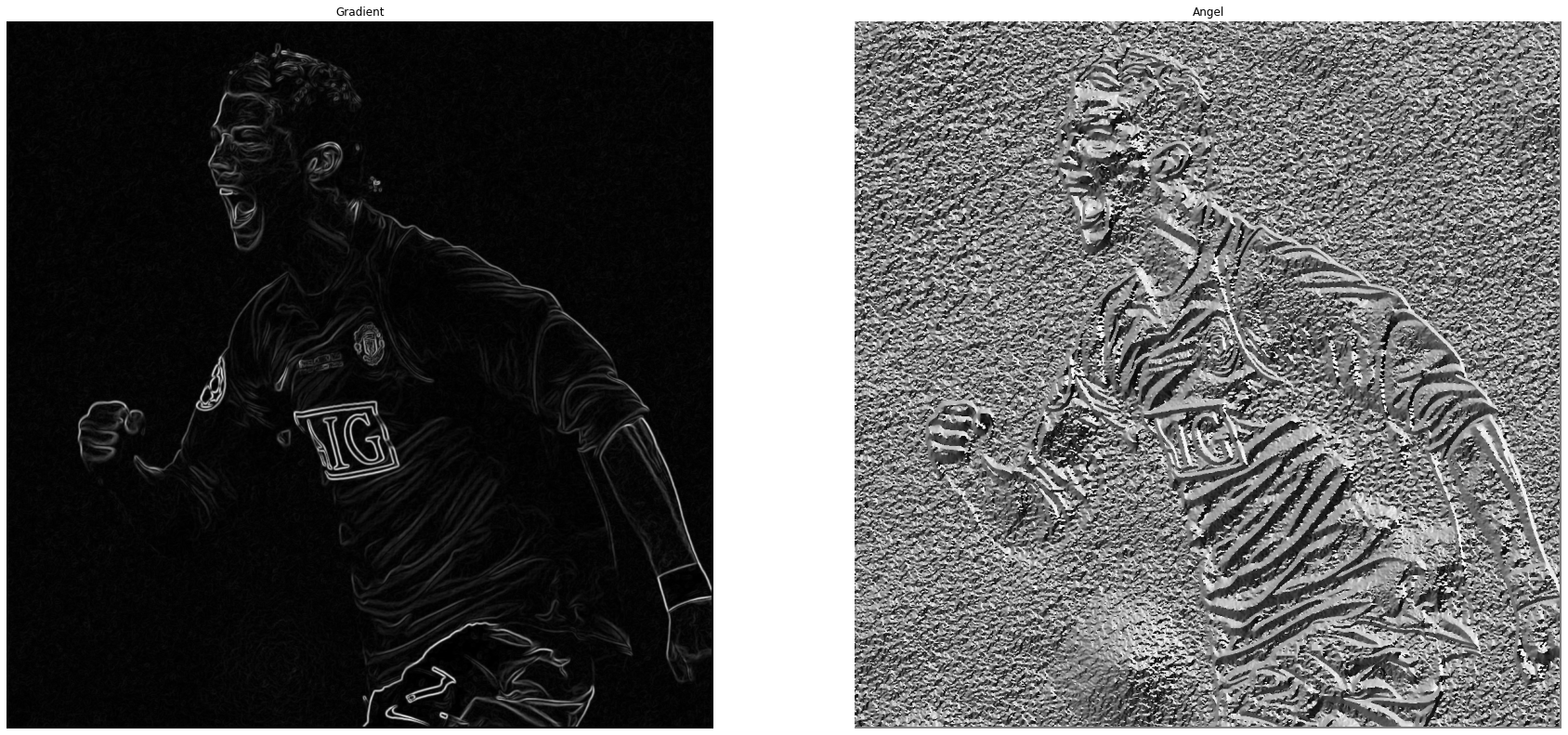
-
Tiếp theo ta sẽ build hàm non-max suppression để xác định chính xác hơn những pixels nào có thể là cạnh. Vì ta sẽ chỉ tính toán 4 hướng với các góc: 0, 45, 90, 135 độ nên ở đây ta sẽ quy ước: 0 - 22.5 độ hoặc 157.5 - 180 độ là góc 0 độ (đường ngang), 22.5 - 67.5 độ là góc 45 độ (đường chéo sang phải), 67.5 - 112.5 độ là góc 90 độ (đường dọc), 112.5 - 157.5 là góc 135 (đường chéo sang trái).
- Tuy nhiên, lưu ý rằng giá trị của ma trận hướng ảnh đang là radian nên ta sẽ đổi sang độ bằng cách nhân 180 chia pi và sau đó cộng 180 với những góc âm sẽ chuyển sang góc tương ứng qua trục hoành.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
def non_max_suppression(img, theta):
"""
Parameters
----------
img : Gradient image
theta : Angle image
Returns
-------
Z : nonMax image
"""
M, N = img.shape
Z = np.zeros((M,N), dtype=np.int32)
angle = theta * 180. / np.pi
angle[angle < 0] += 180
for i in range(1,M-1):
for j in range(1,N-1):
q = 255
r = 255
#angle 0
if (0 <= angle[i,j] < 22.5) or (157.5 <= angle[i,j] <= 180):
q = img[i, j+1]
r = img[i, j-1]
#angle 45
elif (22.5 <= angle[i,j] < 67.5):
q = img[i+1, j-1]
r = img[i-1, j+1]
#angle 90
elif (67.5 <= angle[i,j] < 112.5):
q = img[i+1, j]
r = img[i-1, j]
#angle 135
elif (112.5 <= angle[i,j] < 157.5):
q = img[i-1, j-1]
r = img[i+1, j+1]
if (img[i,j] >= q) and (img[i,j] >= r):
Z[i,j] = img[i,j]
else:
Z[i,j] = 0
return Z
Kết quả thu được sau khi đi qua hàm non_max_suppression: nếu nhìn kĩ ta sẽ thấy các đường nét cạnh của ảnh kết quả rất mảnh và mỏng

- Tiếp theo ta sẽ cần xác định ngưỡng minVal và maxVal cho ảnh và lọc ra các pixels có cường độ mạnh và yếu
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def threshold(img, weak_pixel=75, strong_pixel=255, lowThresholdRatio=0.05, highThresholdRatio=0.15):
"""
Parameters
----------
img : nonMax image
weak_pixel : if weak pixel
strong_pixel : if strong pixel
lowThresholdRatio : ratio of low threshold
highThresholdRatio : ratio of high threshold
Returns
-------
res : thresholded image
"""
maxVal = img.max() * highThresholdRatio
minVal = maxVal * lowThresholdRatio
M, N = img.shape
res = np.zeros((M,N), dtype=np.int32)
strong_i, strong_j = np.where(img >= maxVal)
zeros_i, zeros_j = np.where(img < minVal)
weak_i, weak_j = np.where((img <= maxVal) & (img >= minVal))
res[strong_i, strong_j] = strong_pixel
res[weak_i, weak_j] = weak_pixel
return res

- Cuối cùng ta xác định xem với những pixels đang coi là yếu liệu có thể là cạnh không bằng cách xét vùng xung quanh nó
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def hysteresis(img, weak = 75, strong = 255):
"""
Parameters
----------
img : threholded image
weak : weak pixel value
strong : strong pixel value
Returns
-------
img : final image
"""
M, N = img.shape
for i in range(1, M-1):
for j in range(1, N-1):
if (img[i,j] == weak):
if ((img[i+1, j-1] == strong) or (img[i+1, j] == strong)
or (img[i+1, j+1] == strong) or (img[i, j-1] == strong)
or (img[i, j+1] == strong) or (img[i-1, j-1] == strong)
or (img[i-1, j] == strong) or (img[i-1, j+1] == strong)):
img[i, j] = strong
else:
img[i, j] = 0
return img
Kết quả cuối cùng:

Bây giờ cùng kiểm nghiệm kết quả mình tự làm so với hàm có sẵn trong OpenCV

Kết quả ra của việc tự implement và thư viện có đôi chút khác nhau. Lí do có lẽ đến từ việc xét những ngưỡng minVal và maxVal khác nhau, tuy nhiên những chi tiết bằng cách implement đưa ra nhiều cạnh có thể phát hiện được hơn hàm thư viện nhưng chúng ta chưa thể đánh giá kết quả nào tốt hơn vì có khá nhiều parameters khác nhau ở 2 cách. Nhìn chung, qua đây ta đã hiểu được cách thuật toán Canny và Sobel hoạt động như thế nào, tuy nhiên việc sử dụng hàm có sẵn thường sẽ đưa ra một kết quả tốt và nhanh hơn việc implement nếu không có cải tiến nào mới.
Toàn bộ code sẽ được lưu tại đây.
9. Kết luận
-
Qua bài viết này, mình đã giới thiệu những nội dung cơ bản về không gian màu ảnh, tọa độ một bức ảnh được hiểu trong máy tính.
-
Hơn nữa, các phương pháp tiền xử lí ảnh cơ bản với OpenCV cũng đã được trình bày, có khá nhiều thư viện hiện nay giúp việc tiền xử lí ảnh nhanh hơn và tốt hơn OpenCV nhưng tựu chung thì ý nghĩa các phép biến đổi là như nhau, việc chuẩn hóa màu sắc và độ sáng của ảnh cũng vô cùng quan trọng. Việc tiền xử lí nhưu vậy giúp làm tăng độ giàu về hình ảnh (data augmentation) giúp cho các mô hình Deep Learning trở nên hiệu quả hơn.
-
Ý nghĩa và cách thực hiện phép tích chập trong xử lí ảnh vô cùng quan trọng, nó có thể mở ra rất nhiều bài toán trong thị giác máy tính (computer vision) và ở trong bài mình đã giới thiệu tới 2 thuật toán phát hiện cạnh rất phổ biến: Sobel, Canny algorithm.
-
Bài viết tới đây khá dài nên mình sẽ dừng ở đây. Trong phần 2 của series xử lí ảnh cơ bản, mình sẽ giới thiệu tới các bài toán khác cũng khá hay.
10. Tham khảo
[1] Rosebrook, A., 2016. Practical Python and openCV + case studies. 3rd ed. USA: PyImageSearch.
[2] How the Sobel Operator Works by automaticaddison.com
[3] Sobel Derivatives by OpenCV doc
[4] Smoothing Images by OpenCV doc
[5] Xử lý ảnh - Phát hiện cạnh Canny by minhng.info
[6] Canny Edge Detection Step by Step by towardsdatascience.com
