4. Ôn tập đại số tuyến tính (1/3)
13 Nov 2021Phụ lục:
1. Giới thiệu
Đại số tuyến tính là một mảng toán học rất quan trọng trong machine learning, hầu hết các thuật toán đều dựa trên các tính chất và ứng dụng để tìm ra giải pháp. Tuy nhiên, hiện nay machine learning đã có rất nhiều frameworks và thư viện hỗ trợ nên việc build ra một mô hình machine learning trở nên rất dễ dàng. Đây có thể rất tốt đối với những người đã có kiến thức nền tảng toán căn bản, nhưng đối với mình thời gian đầu tiếp cận thì rất dễ dàng nhưng càng đi sâu thì khá khó khăn với việc những thuật toán nâng cao đều liên quan tới toán học. Vì vậy trong bài hôm nay, mình sẽ tóm gọn các nội dung cơ bản của đại số tuyến tính và thao tác với numpy - một thư viện quan trọng trong machine learning.
Ở trong bài nếu biểu diễn vector là các chữ cái in đậm thường như: $\textbf{a}, \textbf{b}$, các số vô hướng là chữ cái in thường: $a, b$ hoặc các ma trận là chữ cái in hoa đậm: $\textbf{A}, \textbf{B}$
2. Số vô hướng
Số vô hướng (scalar), là giá trị thực không có hướng. Ví dụ số lượng quả táo, cân nặng, chiều cao… Số vô hướng được kí hiệu: $x \in \mathbb{R}$. Để khai báo một số vô hướng với numpy và tính toán:
1
2
3
4
5
6
7
8
9
10
import numpy as np # ĐSTT
x = np.array(3) # Khai báo số vô hướng x
y = np.array(4) # Khai báo số vô hướng y
print("a + b = ", a + b)
>>> a + b = 7
print("a x b = ", a * b)
>>> a x b = 12
3. Vector
Vector thực ra chúng ta đã được học ở cấp 3, như các bài toán tìm vector hình chiếu. Nhưng chưa hiểu rõ ý nghĩa của vector là gì ngoài biết nó có phương, chiều, độ dài và độ lớn. Vector là một khái niệm rất căn bản, nó có thể biểu diễn bất kì đại lượng nào trong thực tế, ví dụ như: diện tích các căn nhà, tuổi của các học sinh trong lớp…
Vector thường được biểu diễn dưới dạng cột array và có ngoặc vuông bao quanh, ví dụ:
\[\mathbf{v} = \begin{bmatrix} 1 \\ 2 \\ -1 \end{bmatrix}\]Vector thường được kí hiệu như sau: $\mathbf{v} \in \mathbb{R}^n$, trong đó $n$ là số lượng phần tử (dimension, length, size) của vector $\mathbf{v}$. Với ví dụ trên $ n = 3$.
Những giá trị bên trong vector còn được gọi là: element, entries, coefficients, components. Để lấy ra giá trị $ith = v_i$ bên trong vector, ta có thể truy xuất tương tự như truy xuất phần tử trong mảng hoặc list (lưu ý: index của vector trong ngôn ngữ lập trình bắt đầu từ $0$ tới $n-1$, trong toán học $1$ tới $n$).
Thao tác với numpy
1
2
3
4
5
6
v = np.array([0,1.1,2.2,3,4]) # Khai báo vector
print(v)
>>> [0,1.1,2.2,3,4]
print(v[2]) # truy xuất phần tử thứ 2
>>> 2.2
Vector đơn vị (unit vector)
Các phần tử bên trong chỉ có duy nhất một phần tử có giá trị bằng 1, còn lại đều bằng 0. Kí hiệu: với vector $\mathbf{e_i}$, giá trị tại phần tử thứ $i$th $=1$, ví dụ:
\[\mathbf{e_1} = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}, \mathbf{e_2} = \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix},\mathbf{e_3} = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}\]3.1. Các thuộc tính của vector
Với việc khai báo vector bằng numpy, ta có thể dễ dàng lấy được một số thuộc tính quan trọng như: độ dài, kiểu dữ liệu, tổng, trung bình, giá trị lớn nhất, giá trị nhỏ nhất bằng cách:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# Độ dài của vector
print("Length of v: ", len(v))
>>> Length of v: 5
# Data type
print("Data type of vector: ",v.dtype)
>>> Data type of vector: float64
# Tổng các giá trị
print("Sum of v: ", v.sum())
>>> Sum of v: 10.3
# Giá trị nhỏ nhất
print("Min of v: ", v.min())
>>> Min of v: 0.0
# Giá trị lớn nhất
print("Max of v: ", v.max())
>>> Max of v: 4.0
# Giá trị trung bình
print("Mean of v: ", v.mean())
>>> Mean of v: 2.06
# Độ lệch chuẩn
print("std of v: ", v.std())
>>> std of v: 1.4022838514366482
3.2. Các phép tính với vector
3.2.1 Cộng, trừ, nhân, chia vector với một số
Với numpy việc tính toán rất dễ dàng, đó là một ứng dụng broadcasting. Cho phép cộng, trừ, nhân, chia trực tiếp. Thao tác với numpy
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
v = np.array([0,1.1,2.2,3,4])
k = 5
# Cộng
print("v + k = ",v+k)
>>> v + k = [5., 6.1, 7.2, 8., 9.]
# Trừ
print("v - k = ",v-k)
>>> v - k = [-5., -3.9, -2.8, -2., -1.]
# Nhân
print("v * k = ",v*k)
>>> v * k = [0., 5.5, 11., 15., 20.]
# Chia
print("v / k = ",v/k)
>>> v / k = [0., 0.22, 0.44, 0.6, 0.8]
3.2.2 Cộng, trừ, nhân, chia giữa 2 vector
Cho 2 vector $\textbf{u}, \textbf{v} \in \mathbb{R}^{n}$. Lưu ý: 2 vector cần phải cùng độ dài (cùng chiều).
– Cộng: $\textbf{u} + \textbf{v} = \textbf{r}$, trong đó $r_i = u_i + s_i$. . Cộng 2 vector theo quy tắc hình bình hành:
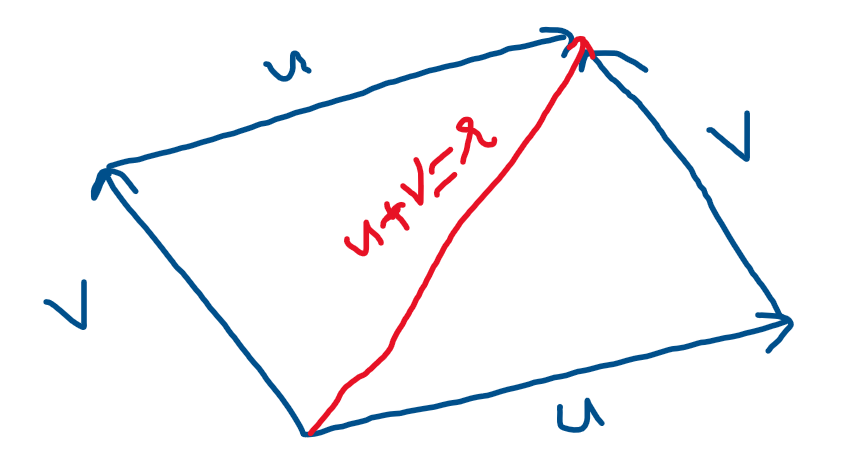
Hình 1: Tổng 2 vector
– Trừ: tương tự phép cộng
– Nhân: Với numpy ta có thể nhân element-wise trực tiếp giữa 2 vector. $\textbf{s} = \textbf{u} * \textbf{v}$ trong đó $s_i = u_i*s_i$.
– Chia: Ta có thể chia trực tiếp 2 vector. $\textbf{s} = \textbf{u} / \textbf{v}$ trong đó $s_i = u_i/s_i$.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
u = np.array([1, 3, 2, 1.8, 1.9])
v = np.array([1, 2.2, 1.2, 1.6, 1.7])
# Cộng
print("u + v: ", u + v)
>>> u + v: [2., 5.2, 3.2, 3.4, 3.6]
# Trừ
print("u - v: ", u - v)
>>> u - v: [0., 0.8, 0.8, 0.2, 0.2]
# Nhân
print("u * v: ", u * v)
>>> u * v: [1., 6.6, 2.4, 2.88, 3.23]
# Chia
print("u / v: ", u / v)
>>> u / v: [1., 1.36363636, 1.66666667, 1.125, 1.11764706]
3.3. Tích vô hướng
Tích vô hướng hay còn một số tên gọi khác như: dot product, inner product, scalar product. Tích vô hướng được sử dụng khá nhiều trong machine learning. Tích vô hướng giữa hai vector $\mathbf{u}, \mathbf{v} \in \mathbb{R}^{n}$ có cùng kích thước là một số vô hướng được ký hiệu là $\langle \mathbf{u}, \mathbf{v} \rangle$ có công thức như sau:
\[\langle \mathbf{u}, \mathbf{v} \rangle = \sum_{i=1}^{n} u_i*v_i\]Ngoài ra để tính độ lớn của vector $\mathbf{r} \in \mathbb{R}^{n}$ ta có thể sử dụng: $\lvert r \rvert = (\sum_{i=1}^{n} r_i^{2})^{\frac{1}{2}} = \langle \mathbf{r}, \mathbf{r} \rangle^{\frac{1}{2}}$. Thao tác với numpy:
1
2
3
4
5
6
7
8
9
10
u = np.array([1, 2, 3])
v = np.array([4, 5, 6])
# dot product
print("<u,v> = ", u.dot(v))
>>> <u,v> = 32
# tính độ lớn của vector
print("Size of u: ",np.sqrt(u.dot(u)))
>>> Size of u: 3.7416573867739413
Lưu ý: từ phần này trở đi, tích vô hướng của 2 vector sẽ biểu diễn bằng dấu “.” và tích element-wise là dấu “*”.
Một số tính chất quan trọng:
-
$\mathbf{u} + \mathbf{v} = \mathbf{v} + \mathbf{u}$
-
$\mathbf{u}.\mathbf{v} = \mathbf{v}.\mathbf{u}$
-
$\mathbf{u}.(\mathbf{t}.\mathbf{v}) = \mathbf{u}.\mathbf{t} + \mathbf{u}.\mathbf{v}$
-
$\mathbf{u}.(\alpha \mathbf{v}) = \alpha (\mathbf{u}.\mathbf{v})$
3.4. Cosine rule
Cho tam giác ABC với độ dài 3 cạnh: AC = a,AB = b, AC = c và 3 vector tương ứng 3 cạnh: $\mathbf{u},\mathbf{v},\mathbf{u-v}$. Góc $\alpha$ là góc tạo bởi AB và AC.
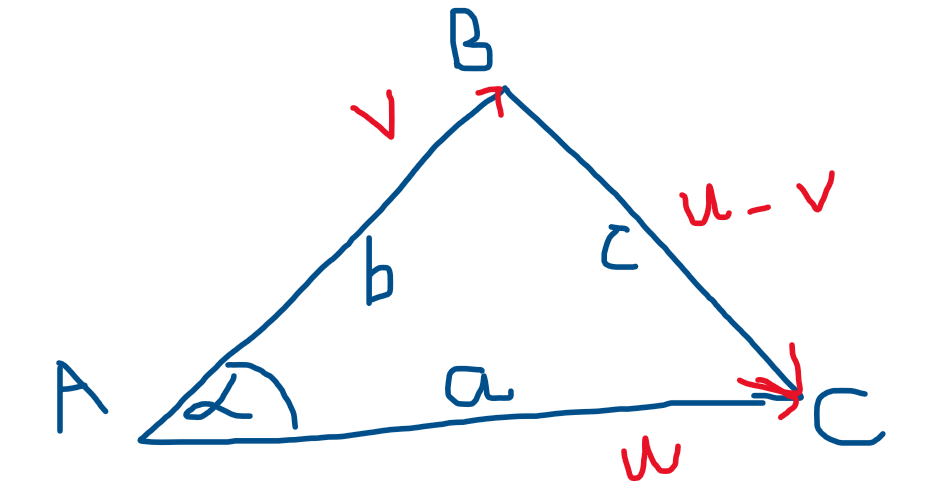
Hình 2: Tam giác ABC
Theo định lý hàm cosin ta có: $c^2 = a^2 + b^2 - 2ab\cos{\alpha}$
\[=> \lvert \mathbf{u-v} \rvert^2 = \lvert \mathbf{u} \rvert^2 + \lvert \mathbf{v} \rvert^2 - 2\lvert \mathbf{u} \rvert \lvert \mathbf{v} \rvert\cos{\alpha} (1)\]Mà \(\lvert \mathbf{u-v} \rvert^2 = (\mathbf{u-v}).(\mathbf{u-v}) = \mathbf{u}.\mathbf{u} + \mathbf{v}.\mathbf{v} - 2\mathbf{u}.\mathbf{v} = \lvert \mathbf{u} \rvert^2 + \lvert \mathbf{v} \rvert^2 - 2\mathbf{u}.\mathbf{v} (2)\)
Từ (1) và (2) $ => \cos{\alpha} = \frac{\mathbf{u}.\mathbf{v}}{\lvert \mathbf{u} \rvert \lvert \mathbf{v} \rvert}$. Suy ra nếu 2 vector vuông góc, tích vô hướng bằng 0.
Việc tính cosine giữa 2 vector có thể so sánh được sử dụng để so sánh độ tương đồng giữa 2 đại lượng.
3.5. Hình chiếu
Cho 2 vector: $\mathbf{u}, \mathbf{v} $. Góc $\alpha$ là góc tạo bởi 2 vector trên. Vector $\mathbf{h}$ là vector hình chiếu của $\mathbf{u}$ xuống $\mathbf{v}$. Tìm vector $\mathbf{h}$ và độ lớn của $\mathbf{h}$.
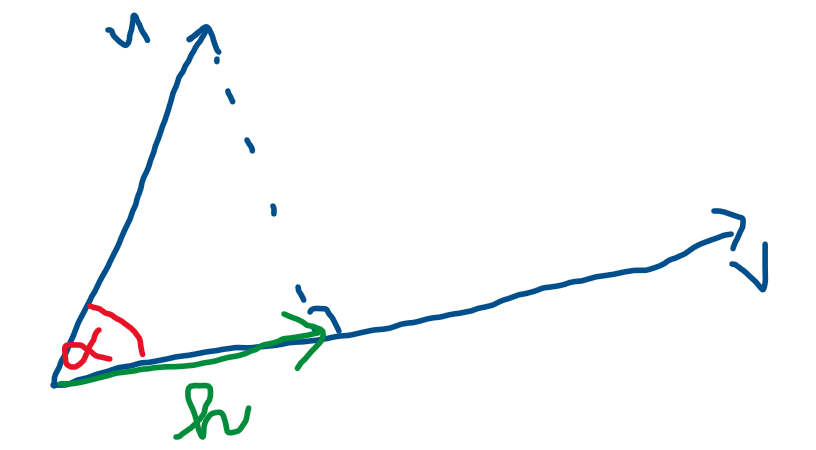
Hình 3: Hình chiếu
Ta có:
\[\cos{\alpha} = \frac{\lvert \mathbf{h}\rvert}{\lvert \mathbf{u} \rvert} = \frac{\mathbf{u}.\mathbf{v}}{\lvert \mathbf{u} \rvert \lvert \mathbf{v} \rvert} => \lvert \mathbf{h}\rvert = \frac{\mathbf{u}.\mathbf{v}}{\lvert \mathbf{u} \rvert}\] \[=> \mathbf{h} = \frac{\mathbf{u}.\mathbf{v}}{\lvert \mathbf{u} \rvert} . \frac{\mathbf{u}}{\lvert \mathbf{u} \rvert}\]4. Norm
Trong machine learning, đôi khi chúng ta cần tính toán độ lớn (size) của một vector. Để tính toán độ lớn đó, ta sẽ sử dụng khái niệm về $\mathbf{norm}$. Công thức được đưa ra như sau:
\[\|\mathbf{x}\|_p = \left(\sum_{i=1}^n \left|x_i \right|^p \right)^{1/p} (1)\]trong đó $p \in \mathbf{R}, p \geq 1$.
Norm của vector $\mathbf{x}$ còn có thể được gọi là khoảng cách từ gốc tọa độ tới tọa độ của vector $\mathbf{x}$. Một số tính chất về norm:
-
\(\|\mathbf{x}\| \geq 0\), dấu bằng xảy ra khi và chỉ khi $\mathbf{x}$ = 0.
-
\(\alpha \|\mathbf{x}\| = \|\mathbf{\alpha x}\|\), việc phóng đại lên véc tơ $\alpha$ lần thì giá trị chuẩn của nó cũng phóng đại lên $\alpha$ lần.
-
\(\|\mathbf{x}\| + \|\mathbf{y}\| \geq \|\mathbf{x + y}\|\), trong đó vector $\mathbf{y}$ cùng chiều vector $\mathbf{x}$. Bất đẳng thức trong tam giác: tổng 2 cạnh luôn lớn hơn cạnh còn lại.
Với công thức (1) là trường hợp tổng quát nhất của norm ($L^p$), còn có tên gọi là Minkowski Norm. Việc thay đổi giá trị $p$ sẽ tạo ra các độ đo khác nhau, một số độ đo thường được sử dụng:
- Với $p = 2$ - Euclidean Norm ($L^2$)
- Với $p = 1$ - Mahattan Norm ($L^1$)
- Với $p \rightarrow \infty$ - Chebyshev Norm
4.1 Khoảng cách
Ở các bài toán về tính khoảng cách giữa 2 điểm bậc THPT, chúng ta đã quen thuộc với khoảng cách Euclidean. Khoảng cách này chính là một norm với giá trị $p = 2$. Cho 2 vector $\mathbf{x}, \mathbf{y} \in \mathbb{R}^n$
\[d_2(\mathbf{x},\mathbf{y}) = ||\mathbf{x - y}||_2\]Với $p = 1$, khoảng cách Mahattan được định nghĩa là norm 1.
\[d_1(\mathbf{x},\mathbf{y}) = ||\mathbf{x - y}||_1\]So sánh sự khác biệt norm 1 và norm 2:
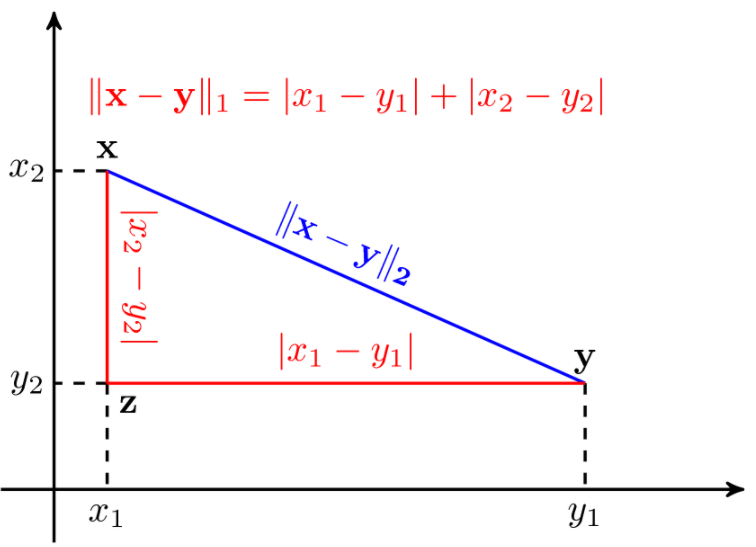
Hình 4: Norm 1 và norm 2 trong không gian 2 chiều (Nguồn: Machine Learning cơ bản)
Norm 2 (màu xanh lục) là đường “chim bay” giữa 2 vector $\mathbf{x}$ và $\mathbf{y}$. Norm 1 thường được sử dụng trong tính toán đồ thị khi không có đường thẳng nối trực tiếp giữa 2 điểm vì vậy ta chỉ có cách đi dọc theo cạnh.
Chứng minh tính chất bất đẳng thức trong tam giác. Cho tam giác và có các vector tọa độ $\mathbf{a},\mathbf{b},\mathbf{b}$ ta có thể suy ra các độ dài cạnh của tam giác như hình sau:
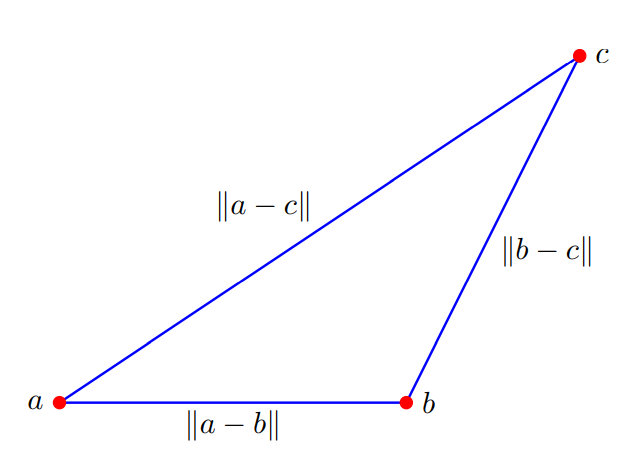
Hình 5: tam giác
Ta có:
\[||\mathbf{a - b}|| + ||\mathbf{b - c}|| \geq ||\mathbf{a - c}||\] \[<=>||\mathbf{a - b}|| + ||\mathbf{b - c}|| \geq ||\mathbf{(a - b) + (b - c)}|\]5. Đánh giá và kết luận
-
Trên đây là những kiến thức cơ bản nhất về vector trong đại số tuyến tính.
-
Các phép toán của vector có rất nhiều ứng dụng trong machine learning như: so sánh độ tương đồng (dựa trên khoảng cách hoặc cosine), giúp việc biểu diễn các features dễ dàng hơn nhằm mục đích tính toán nhanh hơn,…
-
Trong toán học, sẽ không tồn tại các phép chia ma trận hay vector, tuy nhiên với các phép tính trong numpy thì phép chia chỉ có thể thực hiện tương ứng phép nhân nghịch đảo element-wise.
-
2 thuật toán ở bài 6 - K-means và bài 7 - K-nearest neighbors sẽ sử dụng tính chất về norm để giải quyết.
-
Ở phần 2, các kiến thức về ma trận và một số khái niệm chuyên sâu sẽ được trình bày.
6. Tham khảo
[1] Machine Learning cơ bản ebook
[2] Deep AI ebook
