Phụ lục:

• 1. Giới thiệu
• 2. Các định nghĩa trong DBSCAN
• 3. Các loại điểm dữ liệu trong DBSCAN
  • 3.1. Core point
  • 3.2. Boder point
  • 3.3. Noise point
  • 3.4. Ví dụ tổng quát
• 4. Cách thức hoạt động
  • 4.1. Cách thức hoạt động
  • 4.2. Các bước giải bài toán
• 5. Thực nghiệm với Python
  • 5.1. Implement thuật toán
  • 5.2. Nghiệm bằng thư viện scikit-learn
• 6. Cách lựa chọn tham số
• 7. Dự đoán
• 8. Đánh giá và kết luận
• 9. Tham khảo

1. Giới thiệu

Ở bài 7 mình đã trình bày về một thuật toán unsupervised - K-means clustering, mục đích của thuật toán này là gom những cụm dữ liệu có cùng độ tương đồng nào đó về thành một nhóm. Bên cạnh một số ưu điểm của thuật toán này thì một điểm yếu lớn của K-means là toàn bộ dữ liệu sẽ ảnh hưởng tới tâm cụm tìm được tức sẽ bị ảnh hưởng bởi nhiễu (outlier). Vì vậy, trong thuật toán DBSCAN hôm nay mà mình sẽ trình bày sẽ giúp khắc phục được điểm yếu này (phát hiện outlier). Nhưng liệu sau khi đã phát hiện được outlier và bỏ qua chúng thì việc sử dụng thuật toán K-means tiếp theo sẽ tốt hơn? Câu trả lời là có và không. Để hiểu hơn hãy xem ví dụ minh họa về sự khác biệt của 2 thuật toán này:

Hình 1: DBSCAN vs K-means

Như đã thấy ở hình trên, thuật toán DBSCAN có chiến lược phân cụm hoàn toàn khác so với K-means (dữ liệu hình vuông cuối cùng bên phải thể hiện rõ điều này). Từ đây nhận ra rằng với DBSCAN bên trong mỗi cụm sẽ có mật độ dữ liệu cao hơn bên ngoài cụm. Hơn nữa, những điểm outlier thì sẽ có mật độ rất rất thưa.

Vậy thuật toán DBSCAN làm việc như thế nào để tìm ra cụm và điểm nhiễu, mình sẽ trình bày bên dưới.

2. Các định nghĩa trong DBSCAN

Có một số định nghĩa về mặt lí thuyết của thuật toán DBSCAN (phần này cũng không quá quan trọng trong việc hiểu ý tưởng thuật toán, bạn có thể bỏ qua), nên mình sẽ dịch lại các định nghĩa của bài báo gốc:

Định nghĩa 1: Vùng lân cận $\epsilon$ (Epsilon-neighborhood)

Gọi $D$ là tập hợp các điểm trong cơ sở dữ liệu. $p$ là một điểm dữ liệu bất kì thuộc $D$, $\epsilon$ là một hằng số xác định. Tập hợp các điểm lân cận của $p$ có khoảng cách nhỏ hơn $\epsilon$ là:

Định nghĩa 2: Khả năng tiếp cận trực tiếp mật độ (directly density-reachable)

Một điểm $p \in D$ là directly density - reachable từ một điểm $ q ∈ D $ tương ứng với tham số epsilon và minPoints nếu như nó thoả mãn hai điều kiện:

trong đó minPoints cũng là một hằng số xác định nhằm đảm bảo một lượng đủ mật độ để xác định điểm cốt lõi (core point).

Định nghĩa 3: Khả năng tiếp cận mật độ (density-reachable)

Một điểm $p$ là density–reachable từ $q$ khi và chỉ khi có một dây chuyền các điểm $p_1, …, p_n$ với $p_1 = q$ và $p_n = p$ mà $p_i+1$ là directly density – reachable từ $p_i$.

Hai điểm nằm trên biên của một nhóm thì không density–reachable lẫn nhau, bởi vì điều kiện xác định điểm lõi không chứa chúng. Tuy nhiên, trong nhóm sẽ có một điểm lõi mà hai điểm biên đều density–reachable.

Định nghĩa 4: Kết nối mật độ (density-connected)

Một điểm $p$ là density-connected đến một điểm $q$ khi và chỉ khi có một điểm $o$ mà cả hai điểm $p$ và $q$ đều density-reachable từ $o$.

Định nghĩa 5: Nhóm (cluster)

Một nhóm $C$ là một tập con không rỗng của $D$ thỏa các điều kiệu sau:

• $∀ p, q$: nếu $p ∈ C$ và $q$ là density-reachable từ $p$ thì $q ∈ C$.

• $∀ p, q ∈ C: p$ là density-connected từ $q$.

Định nghĩa 6: Nhiễu (noise)

Gọi $C_1, …, C_k$ là các nhóm của tập dữ liệu $D$. Nhiễu là tập hợp tất cả các điểm không thuộc bất kỳ nhóm $C_i$ nào với $i=1, …, k$.

3. Các loại điểm dữ liệu trong DBSCAN

Tóm tắt lại đoạn định nghĩa ở phần trên như sau:

• Vùng lân cận $\epsilon$ là vòng tròn bánh kính bằng $\epsilon$ được vẽ xunh quanh điểm $p \in D$ để quét số lượng điểm rơi bên trong vòng tròn này.

• Sử dụng minPoints làm ngưỡng xác định xem vùng lân cận $\epsilon$ có số điểm dữ liệu tối thiểu để trở thành: core point hay boder point hay noise point.

3.1. Core point

Core point là điểm có số điểm vùng lân cận nhiều hơn hoặc bằng minPoints (tính cả điểm đang xét), ví dụ với minPoints bằng 5 các điểm tròn màu đỏ là core point và màu xanh không phải core point:

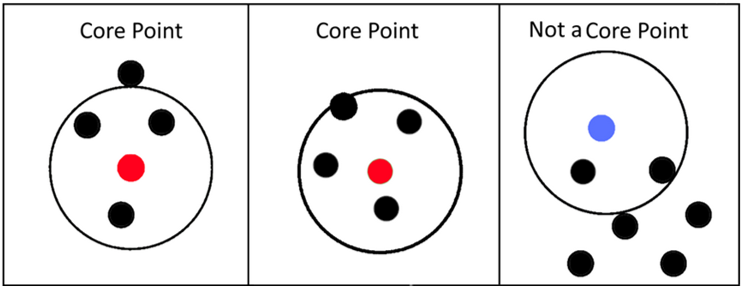
Hình 2: Core point

3.2. Boder point

Boder point là điểm có vùng lân cận chứa ít điểm hơn minPoints nhưng có điểm ở vùng lân cận của điểm cốt lõi (core point), ví dụ minh họa minPoints bằng 5:

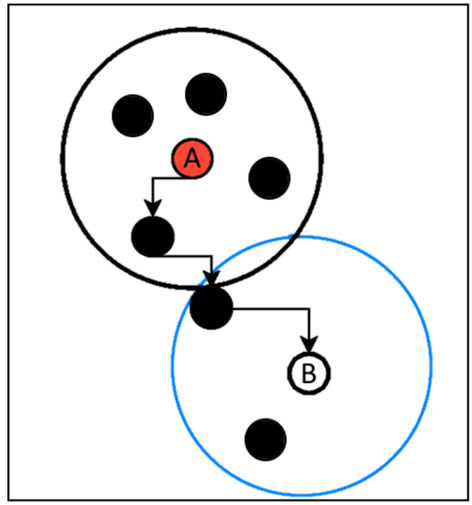
Hình 3: Boder point

3.3. Noise point

Noise point là điểm dữ liệu nhiễu: số lượng điểm lân cận nhỏ hơn minPoints và không có điểm lân cận nào nằm trong vùng lân cận có core point, ví dụ minh họa:

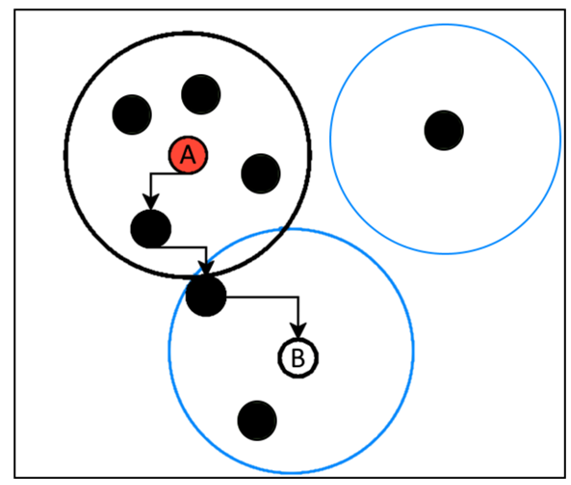
Hình 4: Noise point

3.4. Ví dụ tổng quát

Với minPoints bằng 4, các điểm màu đỏ là core point, màu vàng là Boder point, xanh dương là noise point.

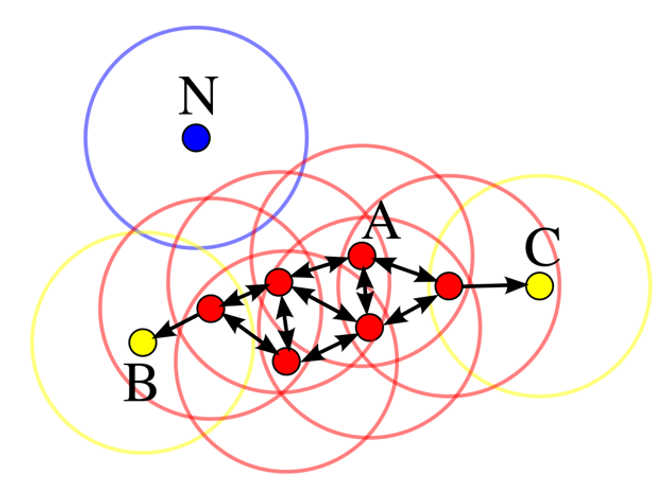
Hình 5: Ví dụ

4. Cách thức hoạt động

4.1. Minh họa hình ảnh

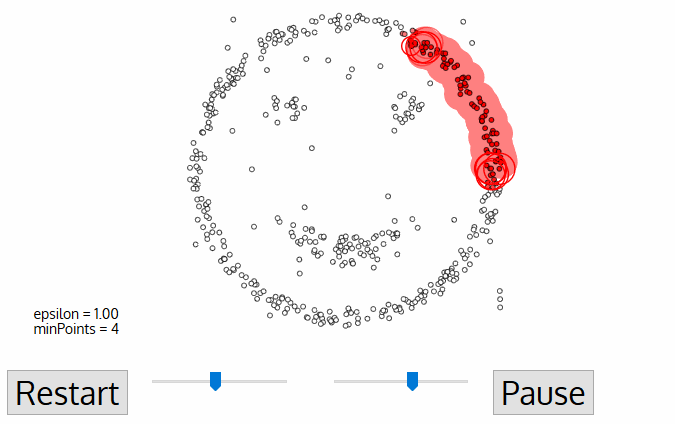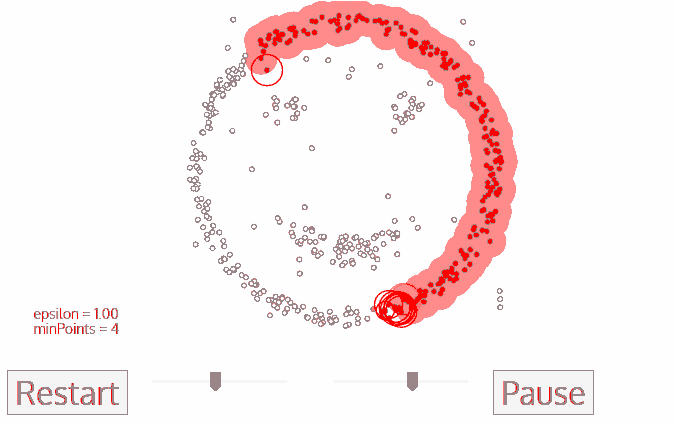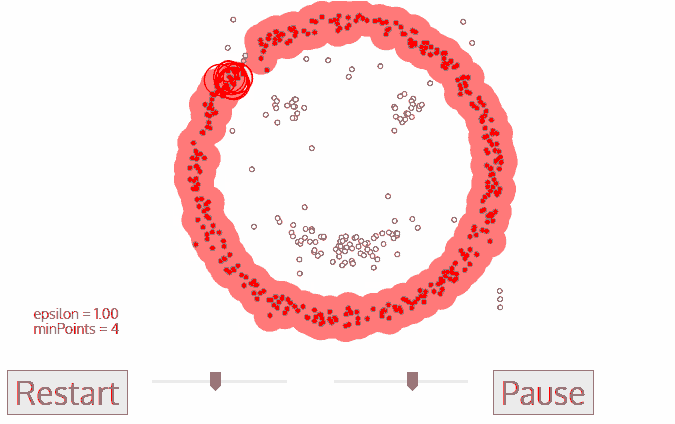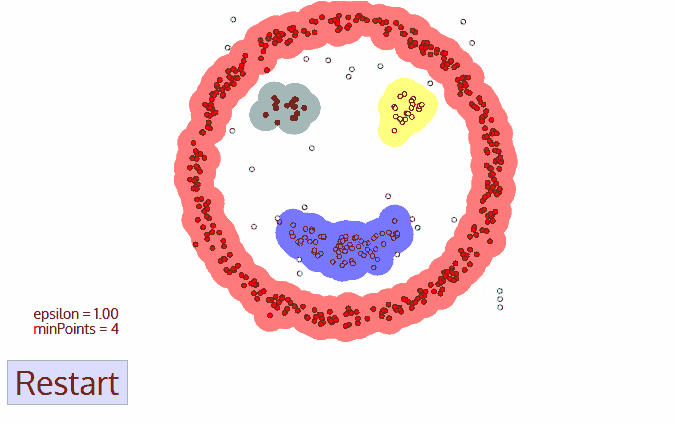
Hình 6: Cách DBSCAN hoạt động

Như bạn đã thấy, thuật toán DBSCAN sẽ dựa trên 2 tham số epsilon và minPoints để tiến hành phân cụm. Quá trình phân cụm sẽ dựa trên một điểm khởi tạo ban đầu, nếu là core point nó sẽ tiếp tục lan truyền mật độ dần dần để mở rộng phạm vi của cụm cho tới khi chạm được hết các điểm border point. Sau khi đã chạm được các điểm border point, thì các điểm chưa được xét sẽ tiếp tục được tính toán dựa trên 2 tham số epsilon và minPoints cho tới khi toàn bộ dữ liệu đã được xét.

4.2. Các bước giải bài toán

Bước 1: Chọn 1 điểm $p$ từ tập dữ liệu

Bước 2: Tìm toàn bộ những vùng lân cận của $p$ với điều kiện thỏa mãn tham số epsilon:

Bước 3: Xác định xem $p$ có thể là core point thỏa mãn điều kiện sau với tham số minPoints:

Bước 4: Nếu $p$ là core point, tiếp tục mở rộng vùng lân cận của các điểm thuộc lân cận của $p$ và xác định như bước 2 và bước 3.

Bước 5: Tiếp thuật cho tới khi toàn bộ dữ liệu đã được xử lí.

Lưu ý: Ở các bước 1, 2, 3, 4 phải thỏa mãn điều kiện điểm $p$ chưa được xét tới bao giờ.

5. Thực nghiệm với Python

Ở phần này, mình sẽ trình bày 2 phương pháp giải: tự implement và thư viện. Sau đó mình sẽ sử dụng kết quả của 2 phương pháp để so sánh xem cách mình tự implement đã đúng chưa. Ngoài ra, mình sẽ sử dụng lại bộ datasets đã thực hiện với bài toán K-means và để so sánh sự khác nhau giữa 2 thuật toán này.

1
2
3
4
5
6
7
8
9
10
11
12
import numpy as np # ĐSTT 
import matplotlib.pyplot as plt # Visualize
from sklearn.datasets import make_blobs # Make the dataset

# Init original centroids
true_centroids = [[1, 1], [-1, -1], [1, -1]] 
# dataset
X, true_labels = make_blobs(n_samples=750, centers=true_centroids, 
                            cluster_std=0.4, random_state=0)
# Visualize dữ liệu
plt.plot(X[:,0],X[:,1],'o')
plt.title('Dataset')

Dataset:

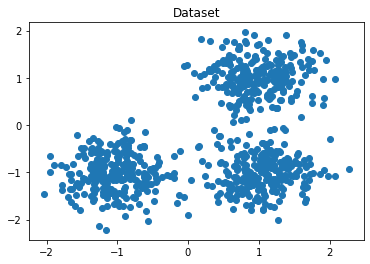
Hình 7: Dataset

5.1. Implement thuật toán

• Trước tiên ta cần một số biến để lưu trữ thông tin cần thiết như: nhãn của toàn tập dữ liệu, đánh dấu xem điểm đang xét tới đã được xét trước đó hay chưa, nhãn của các border point.

1
2
3
labels = np.array([0]*len(true_labels))
visited = np.array([False]*len(true_labels))
labels_border = []

• Hàm tính khoảng cách giữa 2 điểm:

1
2
3
# Calculate distance by norm 2 of two points
def distance(p1,p2):
    return np.linalg.norm(p1-p2,2)

• Hàm lấy ra vùng lân cận của điểm $p$ đang xét tới:

1
2
3
4
5
6
7
# Find nearest neighbors that have distance <= epsilon of point
def nearestNeighbors(data, p, eps):
    neighbors = []
    for i,point in enumerate(data):
        if distance(point, p) <= eps:
            neighbors.append(i)
    return neighbors

• Hàm xử lí thuật toán của DBSCAN, như mình đã trình bày các bước thì ở hàm này nhiệm vụ sẽ đi đánh nhãn cho mỗi điểm dữ liệu dựa trên mật độ và lan rộng từ core point ra các điểm xung quanh từ đó thuật toán sẽ chủ yếu lặp đi lặp lại bước này tới hết toàn bộ dữ liệu được xét (lưu ý các điểm noise ở phần code sẽ có nhãn là -1 và nếu biến visited để kiểm tra xem điểm đó đã được xét hay chưa)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# Main algorithm - DBSCAN
def dbscan(data, eps, minPoints):
    c = 0 # label for each dense density
    for i in range(len(data)):
        p = data[i]
        if visited[i] == True: # this point was visited
            continue
        visited[i] = True # change point status to visited
        neighbors = nearestNeighbors(data, p, eps) # nearest neighbors of point
        if len(neighbors) < minPoints:
            labels[i] = -1 # this is noise point
            continue
        labels[i] = c # core point
        neighbors.remove(i) # remove current core point
        S = neighbors
        # spread from core point
        for j in S:
            if visited[j] == True:
                continue
            labels[j] = c # change point's label of nearest core point
            neighbors = nearestNeighbors(data, data[j], eps) # nearest neighbors of nearest core point
            if len(neighbors) >= minPoints:
                S += neighbors # spread from core point more
            else:
                labels_border.append(j) # this is boder point
            S.remove(j) # remove current core point
            visited[j] = True # change point status to visited
        c += 1 # new cluster initalizes 

• Nếu mới đọc đoạn code hàm dbscan thì có chút bối rối, nhưng bạn có thể vẽ một chút và dựa trên bản chất lan theo mật độ thì nó khá dễ đấy. Bây giờ mình sẽ gọi hàm dbscan và visualize kết quả:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# For visualize
fig, (ax1, ax2) = plt.subplots(1,2, figsize=(10, 4.5))
ax1.plot(X[:, 0], X[:, 1], 'o')
ax1.set_title('Before')

# Main algorithm
eps=0.3
minPoints=10
dbscan(X, eps, minPoints)

# For visualize
n_noise_ = list(labels).count(-1)
core_samples_mask = np.ones_like(labels, dtype=bool)
core_samples_mask[np.array(labels_border)] = False
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
unique_labels = set(labels)
colors = [plt.cm.Spectral(each)
          for each in np.linspace(0, 1, len(unique_labels))]

for k, col in zip(unique_labels, colors):
    if k == -1:
        # Black used for noise.
        col = [0, 0, 0, 1]

    class_member_mask = (labels == k)

    xy = X[class_member_mask & core_samples_mask]
    ax2.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
             markeredgecolor='k', markersize=6)

    xy = X[class_member_mask & ~core_samples_mask]
    ax2.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
             markeredgecolor='k', markersize=6)

ax2.set_title('After')
plt.show()

Kết quả:

• Kết quả khá tốt, những điểm ngoại lai màu đen chính là các outlier ta đã tìm được

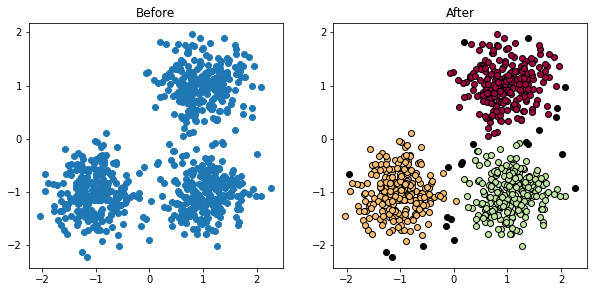
Hình 8: DBSCAN implement

• Mình sẽ in ra số lượng điểm outlier, boder point để lát kiểm tra với thư viện sklearn:

1
2
3
print('Number of outlier: ', n_noise_)
print('Number of boder: ', len(labels_border))
print('Number of core: ', len(labels) - len(labels_border) - n_noise_)

1
2
3
Number of outlier:  22
Number of boder:  56
Number of core:  672

5.2. Nghiệm bằng thư viện scikit-learn

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
import numpy as np 
from sklearn.cluster import DBSCAN 
from sklearn.datasets import make_blobs 
import matplotlib.pyplot as plt 
  
# dataset
centers = [[1, 1], [-1, -1], [1, -1]] 
X, labels_true = make_blobs(n_samples=750, centers=centers, cluster_std=0.4, random_state=0)

# For visualize
fig, (ax1, ax2) = plt.subplots(1,2, figsize=(10, 4.5))
ax1.plot(X[:, 0], X[:, 1], 'o')
ax1.set_title('Before')

# Init DBSCAN model and fit
db = DBSCAN(eps=0.3, min_samples=10).fit(X)

# Attribute values
core_samples_mask = np.zeros_like(db.labels_, dtype=bool)
core_samples_mask[db.core_sample_indices_] = True # db.core_sample_indices_: index of core point
labels = db.labels_ # labels of training dataset
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0) # number of cluster except noise
n_noise_ = list(labels).count(-1) # number of noise data

# For visualize
unique_labels = set(labels)
colors = [plt.cm.Spectral(each)
          for each in np.linspace(0, 1, len(unique_labels))]

for k, col in zip(unique_labels, colors):
    if k == -1:
        # Black used for noise.
        col = [0, 0, 0, 1]

    class_member_mask = (labels == k)

    xy = X[class_member_mask & core_samples_mask]
    ax2.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
             markeredgecolor='k', markersize=14)

    xy = X[class_member_mask & ~core_samples_mask]
    ax2.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
             markeredgecolor='k', markersize=6)

ax2.set_title('After')
plt.show()

Kết quả:

• Như đã thấy thì kết quả của DBSCAN khi sử dụng sklearn cho kết quả giống với cách mình đã implement ở trên

Hình 9: DBSCAN sklearn

• Để chắc chắn mình sẽ in số lượng các điểm outlier, boder, core

1
2
3
print('Number of outlier: ', n_noise_)
print('Number of boder: ', len(labels) - len(db.core_sample_indices_) - n_noise_)
print('Number of core: ', len(db.core_sample_indices_))

1
2
3
Number of outlier:  22
Number of boder:  56
Number of core:  672

Nhận xét:

Như vậy, kết quả của thuật toán DBSCAN giữa việc tự implement và thư viện sklearn đã có cùng một kết quả. Điểm mạnh lớn nhất của thuật toán là đã giúp mô hình có thể phát hiện những điểm dữ liệu, việc này sẽ vô cùng quan trọng trong một bài toán Machine Learning. Ngoài ra, DBSCAN đã giúp phân cụm khá chính xác mà không cần lựa chọn số lượng cụm khởi tạo ban đầu. Tuy nhiên, một vấn đề lớn mà mình chưa hề đề cập đó là chọn 2 tham số epsilon và minPoints. Thuật toán sẽ không thể hoạt động nếu thiếu đi 2 tham số tiên quyết này, vậy làm sao để chọn 2 tham số này phù hợp cho các tập dữ liệu khác nhau, mình sẽ trình bày phần tiếp theo.

6. Cách lựa chọn tham số

Như đã đề cập bên trên, việc chọn tham số epsilon và minPoints sẽ ảnh hưởng trực tiếp tới mô hình, đặc biệt là giá trị epsilon sẽ rất nhạy với dữ liệu vì khi gom một nhóm nhỏ thành vùng lân cận sẽ cần so sánh với giá trị epsilon để quyết định 2 điểm dữ liệu có cùng thuộc một nhóm hay không. Còn việc lựa chọn minPoints sẽ trực tiếp ảnh hưởng tới vấn đề phát hiện outlier.

Các phương pháp chọn tham số:

• minPoints: có một điều chắc chắn rằng giá trị $\textbf{minPoints} \geq 3$, vì nếu $\textbf{minPoints} = 1$ thì mỗi điểm dữ liệu là 1 cụm (vô lí), nếu $\textbf{minPoints} \leq 2$ thì bài toán sẽ chuyển thành kết quả sẽ giống như phân cụm phân cấp (hierarchical clustering) với single linkage với biểu đồ dendrogram được cắt ở độ cao $y = \epsilon$. Do vậy, ở bài báo gốc tác giả đã thử nghiệm và đưa ra với dữ liệu 2 chiều tối thiểu $\textbf{minPoints} = 4$, và tối thiểu $\textbf{minPoints} = 2 \times D$ với dữ liệu trong không gian $D$ chiều. Thường $\textbf{minPoints}$ to sẽ đưa ra các kết quả tốt hơn.

• epsilon: trong bài báo Determination of Optimal Epsilon (Eps) Value on DBSCAN Algorithm to Clustering Data on Peatland Hotspots in Sumatra, tác giả đã đề xuất một phương pháp có thể chọn epsilon ‘có lí hơn’ dựa trên khoảng cách giữa mỗi với điểm tới $n$ điểm gần nhất của nó trên toàn bộ dữ liệu. Tức với $\textbf{minPoints}$ đã tìm được thì ta sẽ đi tìm $k = \textbf{minPoints} - 1$ điểm có khoảng cách gần nhất với mỗi điểm trên toàn bộ dữ liệu. Ứng với mỗi điểm ta sẽ chọn ra khoảng cách lớn nhất của $k$ khoảng cách tìm được và sắp xếp chúng giảm dần, sau đó áp dụng ý tưởng của Elbow method để chọn ra epsilon.

Cụ thể như sau:

Với bộ dữ liệu đã dùng bên trên ta sẽ sử dụng $\textbf{minPoints} = 4$, sử dụng class NearestNeighbors để tìm các điểm gần nhất:

1
2
3
4
5
# Get 4 nearest neighbors for each point in dataset
from sklearn.neighbors import NearestNeighbors
neighbors = 4
neigh = NearestNeighbors(n_neighbors=neighbors)
nbrs = neigh.fit(X) 

Tiếp theo ta sẽ sử dụng hàm kneighbors để lấy ra 2 mảng. 1 mảng $m \times k$ lưu giữ khoảng cách tăng dần với $m$ là số lượng dữ liệu, 1 mảng lưu giữ index tương ứng. Và sau đó sắp xếp khoảng cách lớn nhất tăng dần

1
2
distances, indices = nbrs.kneighbors(X)
distances = np.sort(distances[:,neighbors-1], axis=0)

Bước cuối cùng là xét điểm Elbow, ở đây mình sẽ sử dụng thư viện kneed để tìm ra điểm Elbow chính xác nhất:

1
2
3
4
5
6
7
8
9
10
from kneed import KneeLocator
i = np.arange(len(distances))
knee = KneeLocator(i, distances, S=1, curve='convex', direction='increasing', interp_method='polynomial')
fig = plt.figure(figsize=(5, 5))
knee.plot_knee()
plt.xlabel("Points")
plt.ylabel("Distance")

print('Epsilon = ', distances[knee.knee])
plt.plot(distances)

Kết quả như sau:

1
Epsilon =  0.1618130416143343

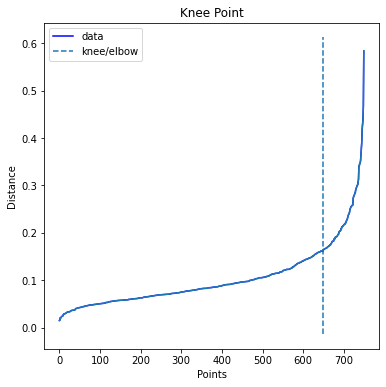
Hình 10: Elbow method

Vậy ta đã xác định minPoints = 4 và epsilon = 0.16, fit vào dữ liệu ta được:

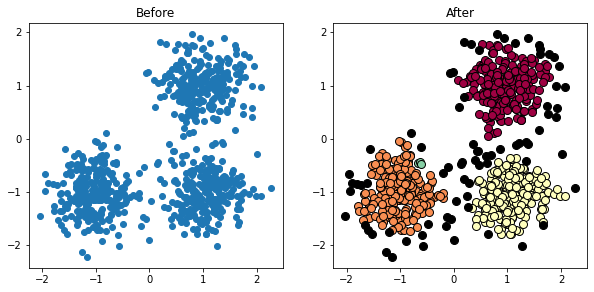
Hình 11: Paramter tuning DBSCAN

Nhận thấy rằng, so với việc chọn epsilon nhỏ đi sẽ ảnh hưởng rất nhiều tới kết quả vì epsilon càng nhỏ thì độ khó tính của thuật toán càng cao, các điểm outlier sẽ xuất hiện nhiều hơn. Vì vậy nếu kết quả bài toán đang đưa ra quá nhiều outlier thì bạn có thể tăng giá epsilon để xem xét. Trong khi đó giá minPoints có thể có thể cố định một giá trị xung quanh $2 \times D$. Tuy nhiên với thuật toán DBSCAN, sklearn không cung cấp hàm predict giúp dự đoán nhãn của một điểm mới đến. Vậy làm sao để xử lí vấn đề này? Mình sẽ trình bày bên dưới.

7. Dự đoán

Vì thuật toán DBSCAN cũng sử dụng khoảng cách để đo lường và sau đó sử dụng epsilon để tìm ra nearest neighbors. Ý tưởng này có đôi chút giống với thuật toán KNN mà mình đã trình bày ở bài 8 - K-nearest neighbors. Thật vậy ta có thể tưởng tượng rằng, sau khi đã sử dụng thuật toán DBSCAN để đánh nhãn cho toàn bộ dữ liệu ban đầu, khi có dữ liệu mới tới ta có thể tìm ra $K$ khoảng cách gần nhất với nó rồi voting xem tần suất nhãn nào nhiều nhất để đưa ra dự đoán nhưng sẽ cần đánh trọng số về khoảng cách, và đây cũng chính là ý tưởng của KNN trong bài toán phân loại.

Vẫn với bộ dữ liệu ban đầu và thêm 1 số điểm cần dự đoán như sau:

1
2
3
4
5
6
7
# dataset
centers = [[1, 1], [-1, -1], [1, -1]] 
X, labels_true = make_blobs(n_samples=750, centers=centers, cluster_std=0.4, random_state=0)
X_new = np.array([[-0.5, 0], [0, 0.5], [1, -0.5], [1, 1]])

plt.scatter(X[:, 0], X[:, 1], c='b')
plt.scatter(X_new[:,0], X_new[:,1],marker="v",c='red')

Hình 12: Dự đoán điểm mới với DBSAN

Sau đó ta sử dụng thuật toán DBSCAN để đánh nhãn và sử dụng những nhãn đó làm cho bài toán phân loại với KNN:

1
2
3
4
5
6
7
8
9
10
11
# Init DBSCAN model and fit
db = DBSCAN(eps=0.18, min_samples=5).fit(X)
labels = db.labels_

# Init KNN model
knn = KNeighborsClassifier(n_neighbors = 5, weights='distance')
knn.fit(X, labels)

# Predict X_new
y_pred = knn.predict(X_new)
print('X_new label predict: ', y_pred)

Kết quả thu được rất chính xác:

1
X_new label predict:  [-1 -1  2  0]

Tuy nhiên, việc chọn số lượng $K$ có thể ảnh hưởng tới kết quả bài toán. Vì nếu có ít nhiễu mà ta lại chọn số lượng giá trị $K$ quá lớn thì sẽ làm cho bài toán khó khăn để dự đoán điểm mới đó là nhiễu. Ngoài ra sủ dụng weights = distance sẽ giúp mô hình tốt hơn.

8. Đánh giá và kết luận

• DBSCAN là một thuật toán vô cùng hay và hiệu quả trong việc phát hiện những outlier, tuy nhiên việc chọn epsilon và minPoints sẽ ảnh hưởng rất nhiều tới kết quả vì vậy ta nên sử dụng phương pháp Elbow ở trên để lựa chọn tham số. Trong trường hợp đoạn cắt Elbow không quá rõ ràng thì có thể sử dụng phương pháp Knee đã trình bày ở trên và tuning giá trị epsilon xung quanh giá trị này.

• DBSCAN không hoạt động tốt cho các bộ dữ liệu thưa thớt hoặc cho các điểm dữ liệu có mật độ khác nhau vì vậy các thuật toán phân cụm phụ thuộc rất nhiều vào sự phân bố của dữ liệu.

• Vì phải tính đi tính lại khoảng cách giữa 2 điểm rất nhiều lần nên thuật toán DBSCAN sẽ bị chậm và kém hiệu quả với những bộ dữ liệu cao chiều.

• Điểm kém hiệu quả của thuật toán là việc tìm nearest neighborhood phải toàn bộ dữ liệu nên độ phức tạp của thuật toán có thể lên tới $O(n^2)$. Vì vậy có một số cải tiến của thuật toán như: HDBSCAN, sử dụng kd-trees…

9. Tham khảo

[1] Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow

[2] A density-based algorithm for discovering clusters in large spatial databases with noise - Original paper

[3] How to Use DBSCAN Effectively by Towardsdatascience

[4] DBSCAN Clustering Algorithm in Machine Learning by Nagesh Singh Chauhan