• 1. Giới thiệu
• 2. Ý tưởng chính
• 3. ID3
  • 3.1. Ý tưởng
  • 3.2. Entropy
  • 3.3. Thuật toán ID3
  • 3.4. Ví dụ minh họa
• 4. Đánh giá và kết luận
• 5. Tham khảo

1. Giới thiệu

Trong thực tế, khi đưa ra một quyết định về một vấn đề nào đó ta thường dựa trên những yếu tố xung quanh để đặt ra những câu hỏi liên quan tới chủ đề mà ta đang quan tâm. Ví dụ trước khi bạn hỏi thằng bạn thân của bạn về cách tán một cô gái là có khả thi hay không, ta cần xem xét liệu có khả thi không dựa trên những gì chàng trai đang có (ở lứa tuổi học sinh) có thể biểu diễn dưới dạng sơ đồ quyết định như sau:

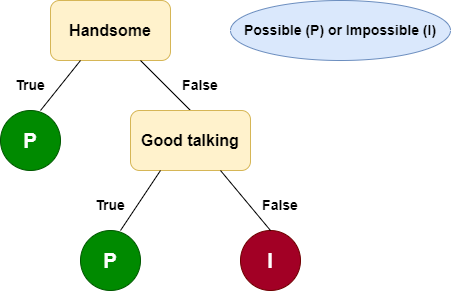
Hình 1: Mức độ khả thi tán cô gái dựa trên câu hỏi

Với hình 1 ta có thể dịch lại như sau:

• Nếu cậu bạn đẹp trai thì khả thi, nếu không cậu ta có khả năng ăn nói trôi chảy thì cũng khả thi và các trường hợp ngược lại còn lại sẽ là không khả thi.

• Ô màu xanh dương là kí hiệu cho có khả thi (P) hoặc không khả thi (I).

• Ô màu vàng là câu hỏi đặt ra.

• Ô màu xanh lục là khả thi (P), màu đỏ là không khả thi (I).

Ta thấy rằng để đưa ra quyết định khả thi hay không khả thi, ta phải đi trả lời liên tiếp các câu hỏi liên quan tới vấn đề cần quyết định. Và đây cũng chính là ý tưởng của thuật toán hôm nay mình sẽ đề cập tới - Decision Tree. Thuật toán này sẽ mô tả những gì mà ta suy nghĩ thường ngày để đưa ra quyết định bằng cách đặt ra những câu hỏi.

2. Ý tưởng chính

Để hiểu rõ các bước mà mô hình Decision Tree làm việc, mình sẽ đưa ra một bộ dữ liệu 2D gồm 2 thuộc tính $x_1$ và $x_2$ như sau (ví dụ này được trích từ Machine Learning cho dữ liệu dạng bảng):

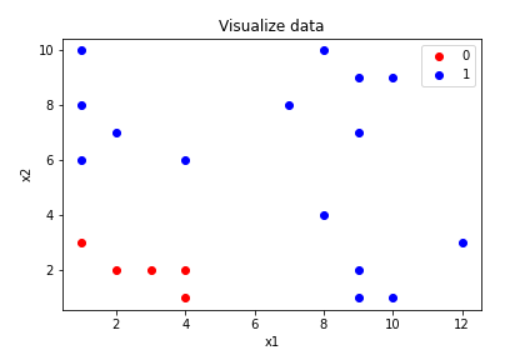
Hình 2: Dataset

Để phân chia tập dữ liệu này thành 2 lớp, ta có thể nghĩ ngay tới thuật toán Logistic Regression để tìm ra 1 đường thẳng ngăn cách. Tuy nhiên, với Decision Tree có thể tìm ra đường nhiều đường phân cách hơn, cụ thể ta xét với ngưỡng và $x_1 > 5$ để chia tập dữ liệu như sau:

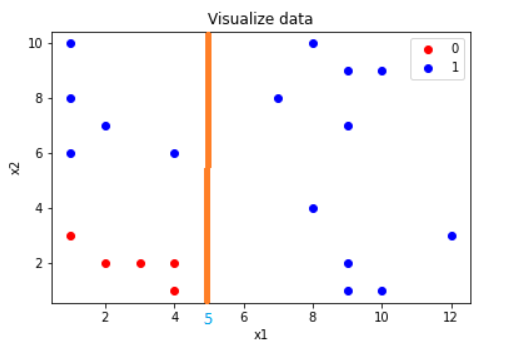
Hình 3: $x_1 > 5$

Từ đây ta có thể suy ra rằng, với bất kì điểm dữ liệu mới nào cần dự đoán chỉ cần có giá trị $x_1 > 5$ sẽ thuộc nhãn 1. Tuy nhiên với $x_1 < 5$ ta có thể thấy rằng vẫn còn có phần dữ liệu nhãn màu xanh dương, vì vậy khi có điểm dữ liệu có $x_1 < 5$ thì rất có thể dự đoán nhầm lẫn. Do đó, ta sẽ tiếp tục xét một ngưỡng $x_2 > 4$ như sau:

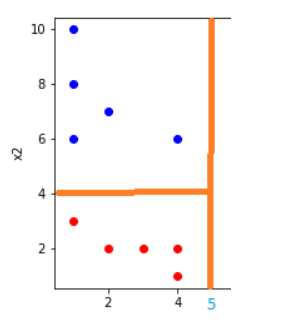
Hình 4: $x_2 > 4$

Lúc này ta có thể nói rằng với các điểm dữ liệu có $x_1 > 5$ thì sẽ thuộc nhãn 1, nếu $x_1 < 5$ mà có $x_2 > 4$ cũng sẽ thuộc nhãn 1 và các trường hợp còn lại thuộc nhãn 0. Và đây cũng chính là cách mà thuật toán Decision Tree sẽ làm:

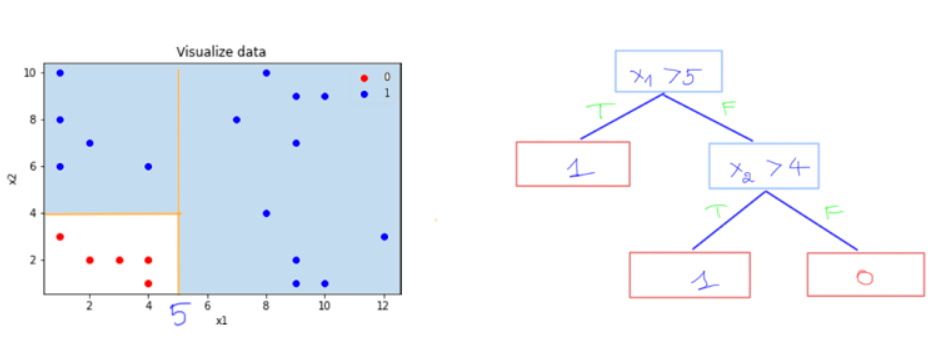
Hình 5: Decision Tree

Ở hình 5 bên phải chính là cây quyết định mà ta đã tạo ra sau khi xét các ngưỡng. Một số kí hiệu về cây quyết định như sau:

• Trong decision tree, các ô hình chữ nhật màu xanh, đỏ trên được gọi là các node

• Các node thể hiện đầu ra màu đỏ (nhãn 1 và 0) được gọi là node lá (leaf node hoặc terminal node)

• Các node thể hiện câu hỏi màu xanh là các non-leaf node

• Non-leaf node trên cùng (câu hỏi đầu tiên) được gọi là node gốc (root node)

• Các non-leaf node có hai hoặc nhiều node con (child node) và các child node có thể là một leaf node hoặc một non-leaf node khác

• Các child node có cùng bố mẹ được gọi là sibling node

Vậy tiêu chí gì để mình tìm được điều kiện đầu tiên? tại sao lại là $x_1$ và tại sao lại là 5 mà không phải là một số khác? Nếu mọi người để ý ở trên thì mình sẽ tạo điều kiện để tách dữ liệu thành 2 phần mà dữ liệu mỗi phần có tính phân tách hơn dữ liệu ban đầu. Ví dụ: điều kiện $x_1 > 5$, tại nhánh đúng thì tất cả các phần tử đều thuộc lớp 1.

• Thế điều kiện $x_1 > 8$ cũng chia nhánh đúng thành toàn lớp 1 sao không chọn? vì nhánh đúng ở điều kiện x1>5 chứa nhiều phần tử lớp 1 hơn và tổng quát hơn nhán đúng của $x_1 > 8$.

• Còn điều kiện $x_1 > 2$ thì cả 2 nhánh con đều chứa dữ liệu của cả lớp 0 và lớp 1.

Từ ví dụ này ta có thể thấy rằng, ở mỗi bước chọn biến ($x_1$) và chọn ngưỡng ($t_1$) là các cách chọn tốt nhất có thể ở mỗi bước. Cách chọn này giống với ý tưởng của thuật toán tham lam (greedy). Cách chọn này có thể không phải là tối ưu, nhưng trực giác cho chúng ta thấy rằng cách làm này sẽ gần với cách làm tối ưu. Ngoài ra, cách làm này khiến cho bài toán cần giải quyết trở nên đơn giản hơn.

Tuy nhiên, tiêu chí chọn $x_1$ và $t_1$ để đưa ra điều kiện phân tách đều dựa trên trực giác mình có thể nhìn thấy được để đưa ra. Nhưng máy tính thì khác, nó cần một độ đo số liệu cụ thể để đưa ra các điều kiện phân tách. Vì vậy, trong bài hôm nay mình sẽ giới thiệu 2 thuật toán phổ biến nhất để làm với Decision Tree: ID3, CART.

3. ID3

Phần này được tham khảo từ phần 2. ID3 - Bài 34: Decision Trees (1): Iterative Dichotomiser 3 - Machine Learning cơ bản, ở phần mình sẽ tóm tắt lại lí thuyết và đưa ra ví dụ để bản thân mình hiểu hơn chứ không implement code. Bạn có thể vào blog trên để theo dõi cách implement.

Source code: Implement ID3 - Machine Learning cơ bản.

Thuật toán ID3 là một giải thuật được ra đời từ khá lâu đời và được sử dụng phổ biến trong bài toán cây nhị phân (binary tree). Thuật toán này được sử dụng cho các bài toán classification mà tất cả các thuộc tính ở dạng categorical. Việc xây dựng một Decision Tree là lần lượt đi chọn các câu hỏi cho từng thuộc tính với mức độ ưu tiên từ trên xuống (top-down) để từ đó tạo nên một cây mang những câu hỏi có tính phân tách dữ liệu tốt nhất. Tất nhiên là có thể kết hợp nhiều thuộc tính để đưa ra câu hỏi và lựa chọn nhưng cách này sẽ khá phức tạp.

3.1. Ý tưởng

Giả sử trong bộ dữ liệu ta có $d$ thuộc tính khác nhau. Và mỗi thuộc tính lại mang những giá trị khác nhau, vậy làm sao để sắp xếp mức độ ưu tiên cho mỗi thuộc tính và đưa ra câu hỏi? Nếu lựa chọn ngẫu nhiên 1 thuộc tính từ $d$, xác suất đúng chỉ là $\frac{1}{d}$ (rất thấp). Vì vậy ta cần xét một tiêu chí nào đó có thể đưa ra cách lựa chọn biến/thuộc tính phù hợp nhất, đây chính là cách ta chọn câu hỏi. Sau mỗi bước lựa chọn được thuộc tính phù hợp nhất ta tiếp tục chia tập dữ liệu vào các child node rồi tiếp tục lại đi tìm thuộc tính phù hợp nhất tiếp theo cho đến khi xuất hiện leaf node, tương ứng nhãn của dữ liệu hoặc gặp một điều kiện dừng nào đó.

Nếu đã từng biết thuật toán greedy (tham lam) thì chắc hẳn bạn đã quen với cách làm này. Ở mỗi bước ta sẽ cố gắng tìm một thuộc tính phù hợp nhất, mặc dù có thể là chưa là tối ưu toàn cục của bài toán. Về thuật toán này, mình sẽ trình bày ở phần Cấu trúc dữ liệu và giải thuật.

Tuy nhiên, trước khi trả về leaf node tức nhãn của dữ liệu ta cần child node có tính phân chia càng cao càng tốt, và tốt nhất thì toàn bộ phân phối rơi vào 1 nhãn tức child node lúc này là leaf node, và đây cũng là chính là kết quả của một chuỗi các thuộc tính/câu hỏi. Do đó, nếu phân phối của các nhãn bằng nhau tức việc phân chia lúc này rất thấp và phải tiếp tục tìm thuộc tính/câu hỏi để phân chia tiếp. Vì vậy, một chỉ số dùng để đánh giá mức độ tinh khiết (purity), hoặc độ vẩn đục (impurity) của một phép phân chia có tên là Entropy.

Đọc đến đây nếu bạn cảm thấy khó hiểu, ‘dont worry about it’ các ví dụ cụ thể sẽ được trình bày bên dưới.

3.2. Entropy

Ở bài 3 - Logistic Regression mình đã giới thiệu về hàm Binary Cross Entropy, hàm này là một trường hợp đặc biệt khi chỉ có 2 nhãn của hàm Cross Entropy. Mục tiêu các hàm này sử dụng để đo sai số xác suất dự báo giữa giá trị dự đoán (prediction) và giá trị thực (ground truth).

Tuy nhiên hàm Entropy sử dụng để đánh giá mức độ tinh khiết và vẩn đục của phép phân chia sẽ chỉ sử dụng mình xác suất dự đoán. Giả sử một sự kiện xảy ra với phân phối xác suất là $\mathbf{p} = (p_1, p_2, \dots, p_C)$ thoả mãn $\sum_{i=1}^{C} p_i = 1$. Khi đó hàm entropy đối với sự kiện trên là:

Nếu sự kiện chỉ có 2 xác suất xảy ra $p$ và $1 - p$ tại 1 node, hàm Entropy có thể viết lại như sau:

Để hiểu rõ mình sẽ visualize hàm $\mathbf{E}(\mathbf{p})$ với các xác suất $p$ như sau:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import numpy as np
import matplotlib.pyplot as plt

# Entropy
def _entropy(p):
  return -(p*np.log2(p)+(1-p)*np.log2((1-p)))

# Probability p
p = np.linspace(0.001, 0.999, 200)

# Visualize
entropy = _entropy(p)
plt.figure(figsize = (12, 8))
plt.plot(p, entropy)
plt.xlabel('p')
plt.ylabel('entropy')
plt.title('Entropy')
plt.show()

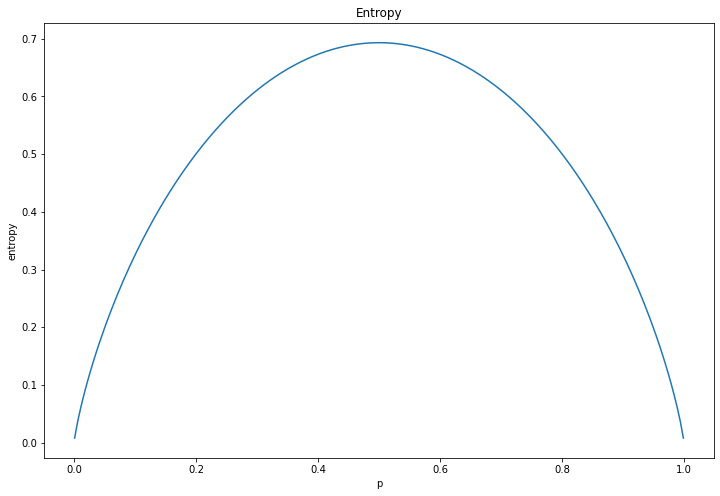
Hình 6: Entropy

Nhận thấy rằng hàm Entropy đạt giá trị cực tiểu tại $p = 1$ và $p = 0$, đạt giá trị cực đại tại $p = 0.5$. Điều này chỉ ra rằng giá trị entropy cực tiểu đạt được khi phân phối $p$ là tinh khiết nhất, tức phân phối hoàn toàn thuộc về một lớp. Trái lại, entropy đạt cực đại khi toàn bộ xác suất thuộc về các lớp là bằng nhau. Một phân phối có entropy càng thấp thì mức độ tinh khiết của phân phối đó sẽ càng lớn.

Với $C > 2$ tức có thể là một cây nhiều nhánh thì điều này vẫn đúng (chứng minh tại đây) tức hàm Entropy là tinh khiết nhất khi có một xác suất $p = 1$ (rơi vào chỉ 1 class).

Lưu ý: khi xuất hiện một xác suất $p_i = 0$ thì ta coi $0\log(0) = 0$.

3.3. Thuật toán ID3

Lúc này ta đã có một độ đo để đưa ra cách lựa chọn cách phân chia phù hợp nhất dựa trên hàm Entropy đã được trình bày bên trên. Thuật toán ID3 được biểu diễn như sau:

Bước 1: Xét bài toán phân loại có $C$ class, node đang tới là một non-leaf node $\mathcal{X}$ với các điểm dữ liệu tạo thành là $\mathcal{S}$ có số lượng phần tử là $N$. $N_c$ là số lượng phần tử của class $c$ với $c = 1, 2, …, C$. Xác suất để mỗi điểm dữ liệu rơi vào một class $c$ được xấp xỉ bằng $\frac{N_c}{N}$. Hàm Entropy dựa trên xác suất được tính như sau:

Bước 2: Yêu cầu đặt ra rằng: Ở non-leaf node này ta cần chọn ra một thuộc tính $x$. Và khi $x$ được chọn thì nhánh tiếp theo sẽ có số lượng child node bằng với số giá trị mà thuộc tính $x$ có. Dựa trên $x$, các điểm dữ liệu trong $\mathcal{S}$ được phân ra thành $K$ child node $\mathcal{S_1},\mathcal{S_2},…,\mathcal{S_K}$ với số điểm trong mỗi child node lần lượt là $m_1,m_2,…,m_K$. Suy ra tổng trọng số Entropy của mỗi child node là:

Thông số đánh giá information gain dựa trên thuộc tính $x$ được tính toán như sau:

Cuối cùng, thuộc tính được lựa chọn $x^*$ là:

tức $x^*$ làm cho information gain lớn nhất hoặc tổng trọng số Entropy nhỏ nhất

Bước 3: Bước 1 và Bước 2 được lặp lại cho tới khi cây tạo ra có thể dự đoán chính xác 100% training data hoặc toàn bộ thuộc tính đã được xét tới. Tuy nhiên cách dừng thuật toán này có thể gây ra Overfiting, ở phần sau mình sẽ bàn luận chi tiết hơn. Chú ý: mỗi thuộc tính chỉ được xuất hiện một lần trên một nhánh.

3.4. Ví dụ minh họa

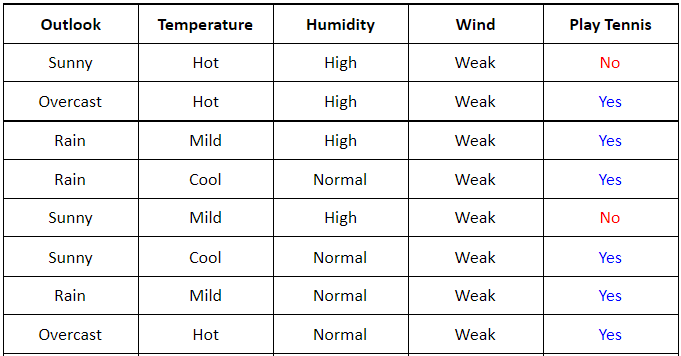
Cho tập dữ liệu sau:

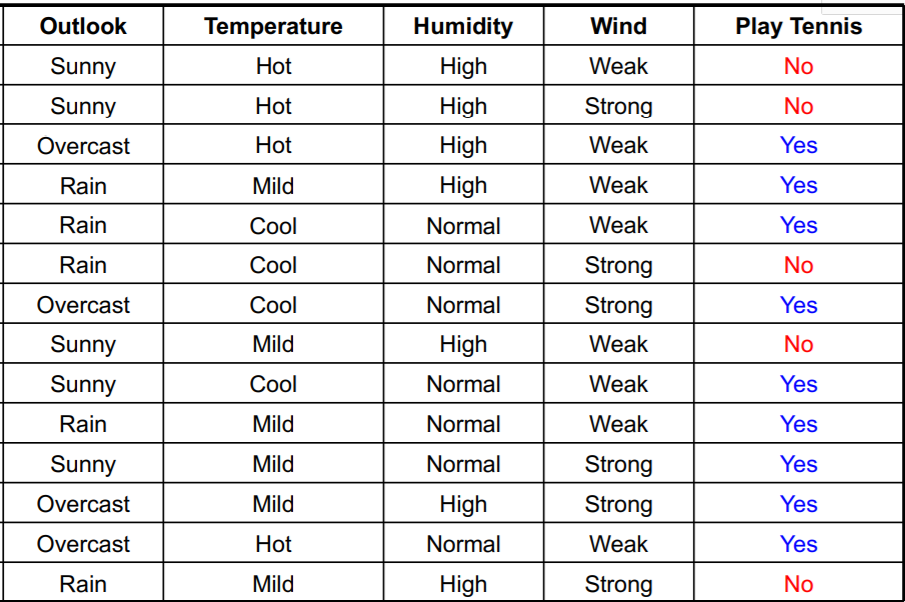
Có 4 thuộc tính về thời tiết:

1. Outlook có thể bằng Sunny hoặc Overcast hoặc Rain.

2. Temperature có thể bằng Hot hoặc Mild hoặc Cool.

3. Humidity có thể bằng High hoặc Normal.

4. Wind có thể bằng Weak hoặc Strong

và Play Tennis là giá trị cần dự đoán dựa vào 4 thuộc tính trên.

Ta sẽ bắt đầu đi tìm thuộc tính và xây dựng một Decision Tree dựa trên thuật toán ID3 đã trình bày bên trên. Đầu tiên ta thấy rằng ở bảng trên có 5 giá trị Play Tennis = No và 9 giá trị Play Tennis = Yes (bước 1) suy ra Entropy tại root node sẽ có giá trị bằng:

Tiếp theo ta sẽ tính toán information gain hoặc tổng trọng số Entropy của 4 thuộc tính Outlook, Temperature, Humidity, Wind để tìm ra thuộc tính phù hợp nhất làm root node.

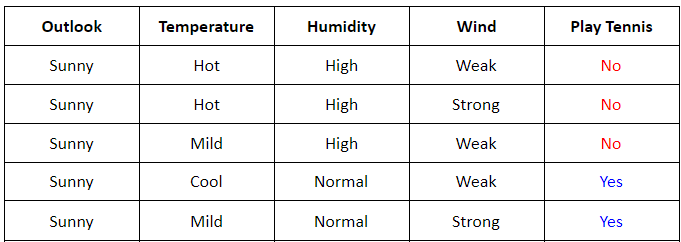
Xét root node là Outlook, ta có thể vẽ lại bảng sau cho dễ tính toán:

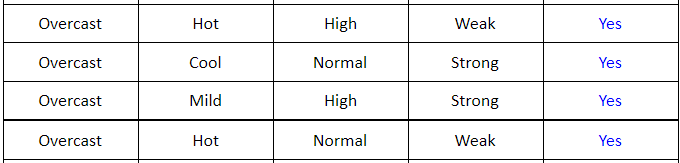
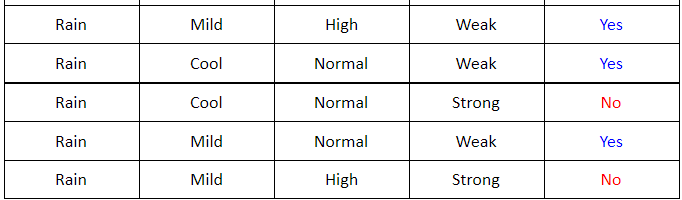
• Ta thấy rằng với root node là Outlook ta sẽ có 3 child node: Sunny, Overcast, Rain. Bây giờ ta cần đi tìm information gain của Outlook dựa trên 3 child node này (bước 2):

  \[\mathbf{G}(\text{outlook}, \mathcal{S}) = \mathbf{E}(\mathcal{S}) - \mathbf{E}(\text{outlook}, \mathcal{S})\]

  mà \(\mathbf{E}(\text{outlook}, \mathcal{S}) = \sum_{k=1}^K \frac{m_k}{N} \mathbf{E}(\mathcal{S}_k)\) trong đó $K = 3, N = 14$.

• Entropy của 3 tập con Sunny, Overcast, Rain trong outlook sẽ được kí hiệu lần lượt là: $\mathbf{E}(\mathcal{S}_s), \mathbf{E}(\mathcal{S}_o), \mathbf{E}(\mathcal{S}_r)$. Suy ra:

  \[\mathbf{E}(\mathcal{S}_s) = - \frac{3}{5}\log\left(\frac{3}{5}\right) - \frac{2}{5}\log\left(\frac{2}{5}\right) \approx 0.97\] \[\mathbf{E}(\mathcal{S}_o) = - \frac{0}{4}\log\left(\frac{0}{4}\right) - \frac{4}{4}\log\left(\frac{4}{4}\right) = 0\] \[\mathbf{E}(\mathcal{S}_r) = - \frac{2}{5}\log\left(\frac{2}{5}\right) - \frac{3}{5}\log\left(\frac{3}{5}\right) \approx 0.97\] \[\mathbf{E}(\text{outlook}, \mathcal{S}) = \frac{5}{14}\mathbf{E}(\mathcal{S}_s) + \frac{4}{14}\mathbf{E}(\mathcal{S}_o) +\frac{5}{14}\mathbf{E}(\mathcal{S}_r) \approx 0.69\] \[\mathbf{G}(\text{outlook}, \mathcal{S}) = 0.94 - 0.69 = 0.25 \quad\quad (5)\]

Xét root node là Wind, tương tự ta có thể vẽ lại bảng sau:

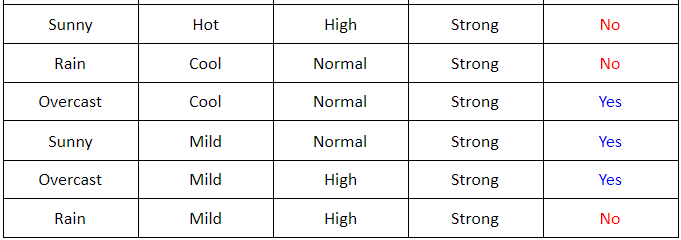
• Ta thấy rằng với root node là Wind ta sẽ có 2 child node: Weak, Strong. Bây giờ ta cần đi tìm information gain của Wind dựa trên child node này (bước 2):

  \[\mathbf{G}(\text{wind}, \mathcal{S}) = \mathbf{E}(\mathcal{S}) - \mathbf{E}(\text{wind}, \mathcal{S})\]

  mà \(\mathbf{E}(\text{wind}, \mathcal{S}) = \sum_{k=1}^K \frac{m_k}{N} \mathbf{E}(\mathcal{S}_k)\) trong đó $K = 2, N = 14$.

• Entropy của Weak, Strong trong Wind sẽ được kí hiệu lần lượt là: $\mathbf{E}(\mathcal{S}_w), \mathbf{E}(\mathcal{S}_s)$. Suy ra:

  \[\mathbf{E}(\mathcal{S}_w) = - \frac{2}{8}\log\left(\frac{2}{8}\right) - \frac{6}{8}\log\left(\frac{6}{8}\right) \approx 0.81\] \[\mathbf{E}(\mathcal{S}_s) = - \frac{3}{6}\log\left(\frac{3}{6}\right) - \frac{3}{6}\log\left(\frac{3}{6}\right) = 1\] \[\mathbf{E}(\text{wind}, \mathcal{S}) = \frac{8}{14}\mathbf{E}(\mathcal{S}_w) + \frac{6}{14}\mathbf{E}(\mathcal{S}_s) \approx 0.89\] \[\mathbf{G}(\text{wind}, \mathcal{S}) = 0.94 - 0.89 = 0.05 \quad\quad (6)\]

Tương tự xét root node cho Temperature và Humidity sẽ thu được các giá trị information gain là:

Từ (5), (6), (7) suy ra thuộc tính sẽ được chọn ở root node là Outlook vì có information gain lớn nhất. Điều này chính xác vì bằng trực giác ta có thể nhìn thấy rằng biến overcast của Outlook đều rơi vào nhãn Yes vì vậy độ tinh khiết tại đây là cao nhất. Lúc này cây của ta sẽ có hình dạng như sau:

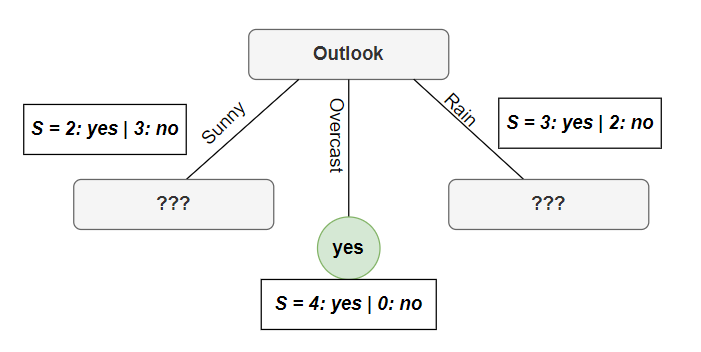
Như đã thấy ở hình trên thì tại root node đã chia làm 3 nhánh overcast, sunny và rain. Tại nhánh overcast thì đã xuất hiện leaf node tức độ tinh khiết lúc này là cao nhất. Tuy nhiên ở 2 nhánh còn lại thì chia được phân chia rõ ràng giữa 2 lớp (vẩn đục) vì vậy ta sẽ tiếp tục xét lần lượt các thuộc tính còn lại (ngoại trừ outlook) để phân chia cho tới khi độ tinh khiết cao nhất.

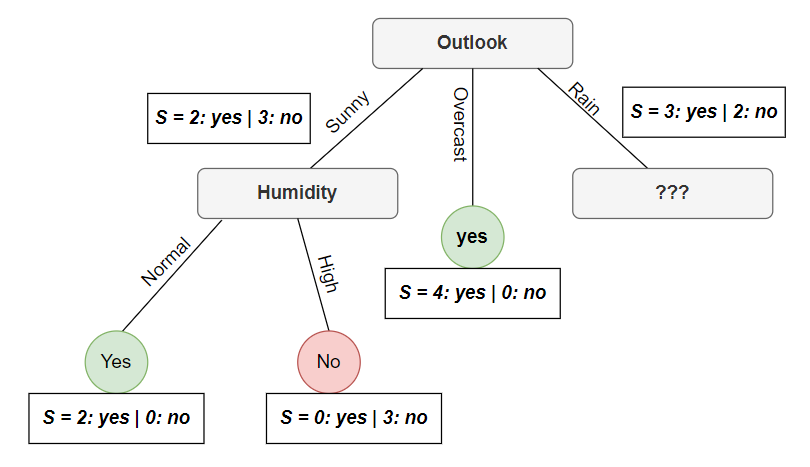
Xét nhánh sunny:

• Giá trị Entropy của $\mathcal{S}$ tại nhánh sunny là:

• Nếu chọn thuộc tính Humidity (nhìn nhanh thì bạn có thể thấy được thuộc tính này phân tách rất rõ ràng khi được phân loại tuy nhiên mình vẫn sẽ viết toàn bộ cách tính), Entropy của High, Normal sẽ được kí hiệu lần lượt là: $\mathbf{E}(\mathcal{S}_h), \mathbf{E}(\mathcal{S}_n)$. Suy ra:

• Tính toán tương tự cho 2 thuộc tính Temperature và Wind bạn sẽ nhận được giá information gain lần lượt là: $0.57, 0.019$. So sánh với information gain của Humidity thì ta sẽ chọn node này là Humidity và cây của ta lúc này sẽ được như sau:

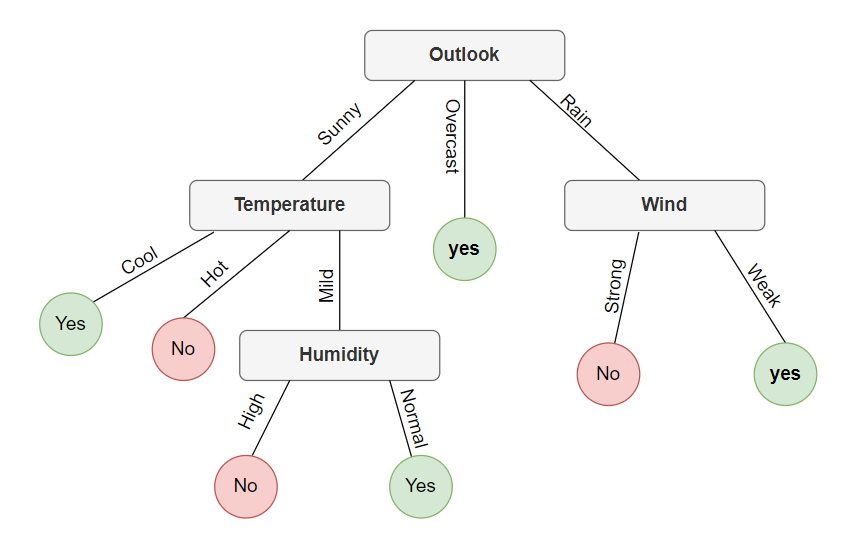
Tương tự xét nhánh rain ta sẽ thu được một cây hoàn chỉnh với các leaf node xuất hiện như sau:

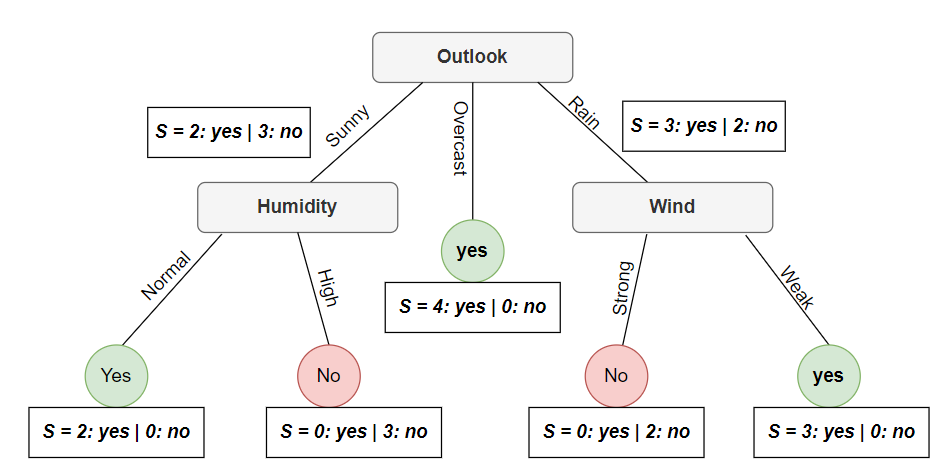
Kết luận: Tới đây một Decision Tree đã được hoàn thiện bằng thuật toán ID3, khi có một điểm dữ liệu mới ta sẽ bắt đầu hỏi các câu hỏi từ trên xuống (từ root node) để xác định nhãn cuối cùng. Nếu bạn thử lại toàn bộ dữ liệu ở trên ví dụ thì sẽ thấy với cây ta tạo được sẽ dự đoán chính xác 100% và nếu dụ một dữ liệu như sau: Outlook: Rain, Temperature: Hot, Humidity: Normal, Wind: Strong thì sẽ có nhãn là No.

4. Đánh giá và kết luận

• ID3 sử dụng thuật toán Greedy (tham lam) dựa trên rằng buộc là information gain hoặc tổng trọng số Entropy của một thuộc tính để từ đó chọn ra một thuộc tính có thể phân chia dữ liệu theo nhãn phù hợp nhất ở mỗi node được chọn. Tuy nhiên điểm yếu của thuật toán Greedy là đôi khi nó không tìm ra một nghiệm tối ưu toàn cục mà chỉ là cục bộ. Vì vậy ID3 chưa chắc đã tạo nên một cây tối ưu nhất, ví dụ với bộ dữ liệu bên trên vẫn tồn tại một số sơ đồ cây khác đảm bảo dự đoán chính xác 100% training data như sau:

• Vậy ID3 sẽ lựa chọn cây nào? ID3 sẽ lựa chọn duy nhất một cây thỏa mãn điều kiện hỗn tạp (information gain lớn nhất) nhỏ nhất, vì vậy cây tìm ra sẽ dựa trên thuộc tính mà ID3 tìm ra và lựa chọn làm non-leaf node ở mỗi lần lặp.

• Với ID3 cây có xu hướng mở rộng bề ngang (lùn, thấp) vì những thuộc tính có information gain cao sẽ càng gần root node. Thật vậy, giả sử khi bạn muốn dựa trên một số thông tin cho trước để đưa ra dự đoán xem đó là ai trong lớp học. Các thông tin này có thể bao gồm: Sở thích, thói quen, giới tính, ngày sinh… giả sử rằng trong lớp không có ai trùng ngày sinh với nhau thì ta chỉ cần mỗi thông tin/thuộc tính này để có thể đưa ra dự đoán chính xác 100%. Vì tính hỗn tạp của thuộc tính lúc này là không có tức tổng trọng số hàm Entropy lúc này bằng không thì information gain là lớn nhất. Vì vậy thuộc tính mà có càng nhiều giá trị thường có xu thế nằm gần root node.

• Thuật toán ID3 làm việc với dữ liệu dạng categorical tuy nhiên với dữ liệu dạng liên tục ta có thể biến đổi một chút để đưa thành dạng categorical. Ví dụ bạn có dữ liệu thuộc tính điểm là: $1,2,3,…10$ bạn có thể chia thành 3 khoảng: $1 - 4$ là weak, $5 - 7$ là median, $8 - 10$ là high. Tuy nhiên cách này sẽ làm mất đi khá nhiều ý nghĩa của dữ liệu. Đặc biệt khi phân chia kiểu này thì sẽ rất dễ bị nhầm lẫn khi dự đoán vì vô tình ta đã coi điểm $1 = 4$.

Vì bài tới đây khá dài nên mình sẽ trình bày về thuật toán CART ở bài sau cũng như vấn đề mà các thuật toán Decision Tree gặp phải.

5. Tham khảo

[1] Bài 34: Decision Trees (1): Iterative Dichotomiser 3 - Machine Learning cơ bản by Vu Huu Tiep

[2] Decision Tree algorithm by Tuan Nguyen

[3] Decision Tree - Machine Learning and Data Mining by Khoat Than