Phụ lục:

• 1. Giới thiệu
• 2. Lập công thức chung
• 3. Thực nghiệm với Python
• 4. Một số vấn đề lưu ý
  • 4.1. Learning rate
  • 4.2. Cost function
  • 4.3. Feature scaling
• 5. Đánh giá và kết luận
• 6. Tham khảo

1. Giới thiệu

Ở bài 1 - Linear Regression chúng ta đã đi tìm nghiệm cho bài toán bằng các phương pháp sử dụng hình học, đại số tuyến tính kết hợp đạo hàm. Nhưng điểm yếu còn tồn tại đó là ta phải tính ma trận nghịch đảo (trong nhiều trường hợp không thể tìm trực tiếp) làm chậm về tốc độ tính toán, tràn bộ nhớ với những tập dữ liệu lớn đặc biệt là khi số lượng features của dữ liệu rất lớn. Thuật toán Gradient Descent có thể cải thiện hơn mà vẫn đạt độ hiệu quả khá cao, hơn nữa Gradient Descent là cơ sở của rất nhiều thuật toán tối ưu trong Machine Learning/Deep Learning.

Ý tưởng của thuật toán Gradient Descent chính là việc ứng dụng đạo hàm để tìm nghiệm tối ưu. Để dễ dàng giải thích, hãy xem đồ thị của phương trình $f(x) = x^4 - 5x^2 - x + 3$

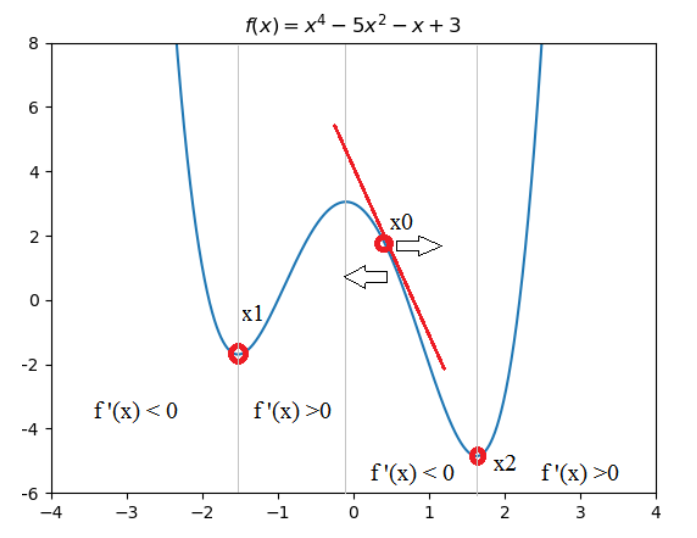
Hình 1: Đồ thị hàm số

Để tìm giá trị nhỏ nhất cho hàm $f(x)$ trên. Ta thường tìm đạo hàm $f’(x)$ và tìm nghiệm $f’(x) = 0$. Và sau đó thế lại các nghiệm đã tìm được vào hàm $f(x)$ để lấy giá trị nhỏ nhất. Trong machine learning, quá trình thế này có thể gọi là so sánh các local optimum để lấy được global optimum. Ở đồ thị Hình 1 ta có nghiệm $x_1$ là nghiệm local optimum và $x_2$ là nghiệm global optimum. Nhưng trong các bài toán machine learning rất khó để có thể tìm đạo hàm rồi đi tìm từng nghiệm, vì vậy ta sẽ cố gắng tìm các điểm local optimum nào đó và coi nó là nghiệm chấp nhận được cho bài toán.

Xét điểm $x_0$ trên đồ thị Hình 1 là nghiệm khởi tạo ban đầu, điều ta cần chính là làm sao để $x_0$ tiến gần tới $x_2$. Đây chính là cách mà thuật toán Gradient Descent sẽ làm. Qua nhiều lần lặp với công thức $x_0 := x_0 - \alpha f’(x_0)$ trong đó hằng số dương $\alpha$ được gọi là learning rate cần được khởi tạo ban đầu. Ta thấy $f’(x_0) < 0 <=> \alpha f’(x_0) < 0 =>$ $x_0$ sẽ ngày càng tiến đến vị trí $x_2$ và làm cho $f(x_0)$ giảm dần. Tức ta cần di chuyển nghiệm $x_0$ ngược dấu với đạo hàm đang xét.

2. Lập công thức chung

Để ứng dụng thuật toán Gradient Descent, ở bài này mình sẽ trình cách sử dụng thuật toán Gradient Descent để giải quyết bài toán hồi quy đã được xử lí bằng cách giải và tìm nghiệm trực tiếp ở bài 1 - Linear Regression. Vì vậy hàm dự đoán và hàm mất mát vẫn tương tự. Như đã trình bày bên trên, ta sẽ sử dụng phương pháp cập nhật nghiệm ban đầu khởi tạo nhiều lần nhằm giảm giá trị hàm cost nhất có thể.

Bài toán dự đoán giá nhà dựa trên diện tích với $m$ mẫu dữ liệu, ta có:

Các bước để xử lí bài toán:

• Bước 1: Khởi tạo nghiệm $W$, learning rate $\alpha$, số lần lặp $\textbf{iterations}$.
• Bước 2: Cập nhật $W := W - \alpha \frac{dJ}{dW}$.
• Bước 3: Dừng lại khi hết $\textbf{iterations}$ lần lặp.

Ở bước 3, có khá nhiều cách để dừng vòng lặp như:

• Giới hạn số lần lặp (như ở trên).
• Giới hạn giá trị hàm cost - J.
• Giới hạn hiệu giá trị của hàm cost tại 2 lần gần nhất.

Nhưng trong thực thế, các giá trị hàm cost sẽ khá khó để biết nó thay đổi như thế nào khi train model, cách giới hạn số vòng lặp và đưa ra một số rules để thuật toán dừng (callbacks) là đơn giản nhất mà vẫn đạt được các giá trị tốt.

3. Thực nghiệm với Python

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
import numpy as np # ĐSTT
import matplotlib.pyplot as plt # Visualize

# Hàm này sử dụng để tìm nghiệm W và cost sau mỗi lần lặp
# vì vậy W và cost cuối cùng sẽ là nghiệm và giá trị cost cho bài toán
def process(W, X, Y, learning_rate, num_iterations):
    m = X.shape[0]
    ones = np.ones((m, 1))
    X = np.concatenate((ones, X),axis=1)
    cost = np.zeros((num_iterations,1))
    W_list = []
    for i in range(num_iterations):
        dist = np.dot(X,W) - Y
        cost[i] = 0.5*(1/m)*np.sum(dist*dist)
        W = W - learning_rate/m*(np.dot(X.T,dist))
        W_list.append(W)
    return W_list,cost

# Hàm này sử dụng để dự đoán khi có một giá trị x0
def predict(W,x0):
    w0,w1 = W[0],W[1]
    y0 = w0 + w1*x0
    return y0

# Dùng để visualize đường thẳng cần tìm
def draw_line(min_x,max_x,W,color='r'):
    min_y = predict(W,min_x)
    max_y = predict(W,max_x)
    plt.plot((min_x,max_x),(min_y,max_y),color)

def main():
    # Dữ liệu
    X = np.array([[2,9,7,9,11,16,25,23,22,29,29,35,37,40,46]]).T
    Y = np.array([[2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]]).T
    
    # Visualize dữ liệu
    plt.scatter(X, Y)
    min_x,max_x = 2,46 # Điểm để visualize
    
    # Khởi tạo nghiệm
    W = np.array([[1.],
                  [2.]])
    
    # leaning rate - alpha
    learning_rate = 0.0001
    
    # số lần lặp iterations
    num_iterations = 100
    
    # Visualize đường khởi tạo
    draw_line(min_x, max_x, W,color='black')
    
    # Tìm nghiệm
    W_list,cost = process(W, X, Y, learning_rate, num_iterations)
    
    # Visualize đường thẳng các nghiệm tìm được
    for W in W_list:
        draw_line(min_x,max_x,W,'blue')
        
    # Visualize đường kết quả
    draw_line(min_x,max_x,W_list[-1],'red')
    
    title = ['init line','update line']
    plt.tight_layout()
    plt.legend(title)
    plt.xlabel('Diện tích')
    plt.ylabel('Giá')
    plt.show()

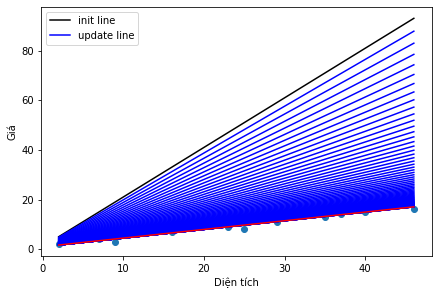
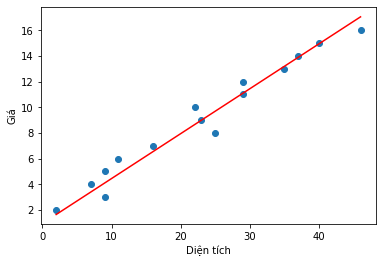
Hình 2: Visualize các nghiệm sau mỗi lần cập nhật và đường thẳng tương ứng

Ta thấy đường màu đen chính là nghiệm mà ta khởi tạo, các đường màu xanh chính là nghiệm sau mỗi cập nhật theo công thức Gradient Descent (ở bước 2). Đường màu đỏ chính là nghiệm cuối cùng của bài toán.

Ở đây ta thấy sau 100 lần lặp thì nghiệm cuối cùng đã tìm được, nghiệm cho bài toán khá tốt, đường tìm được khá giống với nghiệm tìm theo công thức ở bài 1 - Linear Regression. Hãy xem hàm mất mát biến đổi như thế nào sau mỗi lần lặp

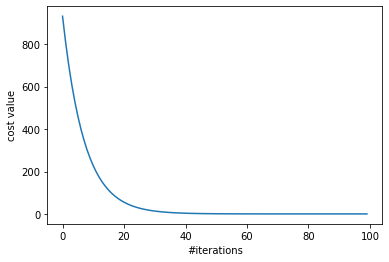
Hình 3: Visualize cost function

Trục ngang là giá trị số lần lặp của thuật toán, trục dọc là giá trị hàm cost sau mỗi vòng lặp. Nhận thấy rằng, tại vòng lặp thứ 40 đổ đi gần như hàm cost vẫn giữ nguyên giá trị rất gần 0, tức ta đã đạt được mong muốn rằng giá trị hàm cost càng nhỏ càng tốt (gần 0). Tuy nhiên, máy tính vẫn thực thi 60 vòng lặp mà các giá trị của hàm cost gần như không thay đổi vì vậy ta sẽ các chiến thuật để dừng vòng lặp là callbacks hoặc tính toán 2 giá trị cost gần nhất, về vấn đề này mình sẽ trình bày ở bài khác.

4. Một số vấn đề lưu ý

4.1. Learning rate

Có một điều khá qua trọng mà chưa được nhắc tới ở phần trên đó là việc chọn learning rate. Hãy xem sự ảnh hưởng của chọn learning rate

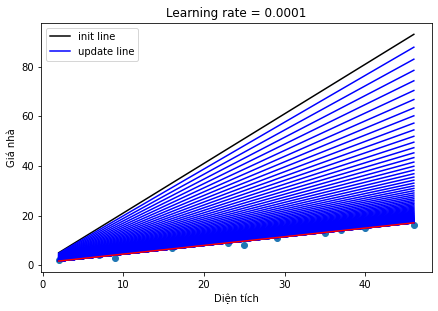
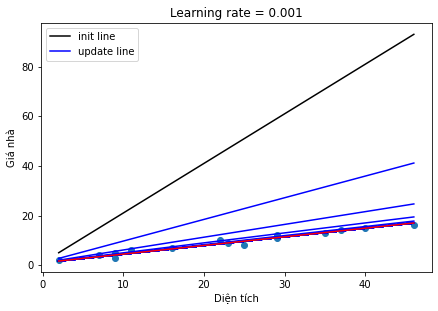
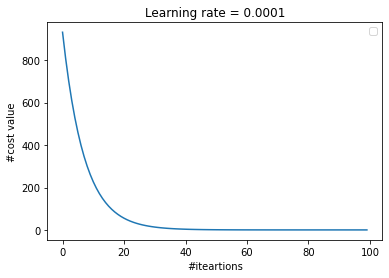
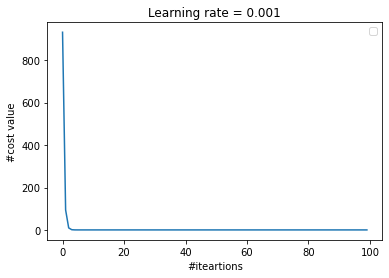
Hình 4: So sánh chọn learning rate

Ta thấy ở Hình 4, việc lựa chọn các learning rate khác nhau sẽ đem đến các kết quả khác nhau. Đây cũng là một hạn chế của thuật toán này khi phải tuning lại giá trị của learning rate nhiều lần. Nhưng nếu chọn learning rate quá nhỏ sẽ làm cho quá trình hội tụ (tức đạt tới giá trị nghiệm tối ưu) rất rất chậm, hoặc nếu quá to thì sẽ có thể không bao giờ đạt tới

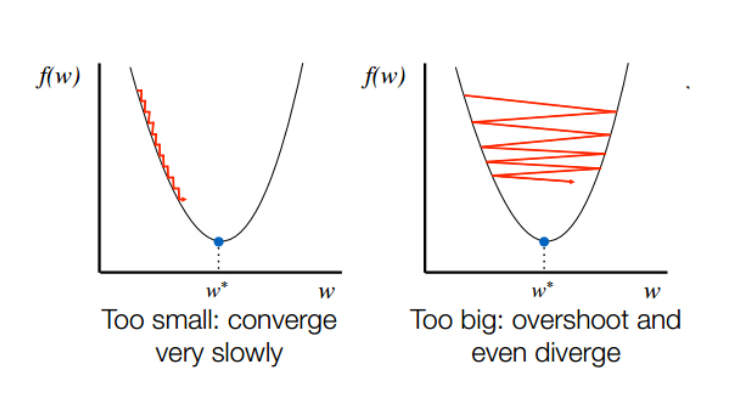
Hình 5: Hình trái - learning quá nhỏ, Hình phải - learning rate quá to

4.2. Cost function

Trong bài 1 và bài 2 này ta đã làm quen với Cost function là trung bình bình phương lỗi của toàn bộ dữ liệu, tên gọi tiếng Anh là: Mean Squared Error. Vậy tại sao hàm Cost function này lại được sử dụng mà không phải hàm số nào khác cũng có thể đo lường sai số giữa giá trị thực và giá trị dự đoán, cùng xem ví dụ sau:

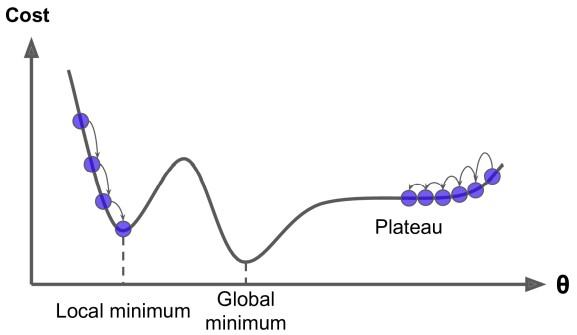
Hình 6: Gradient Descent pitfalls (Nguồn: Hands-on machine learning)

Ở Hình 6, giả sử ta khởi tạo giá trị nghiệm ban đầu phía bên trái của điểm Local minimum thì hàm cost sẽ hội tụ tại đúng điểm Local minimum và rất khó có thể tới vươn tới điểm global minimum (gần như không thể). Mặt khác, nếu nghiệm ban đầu ta khởi tạo nằm trên đoạn Plateau thì việc cập nhật GD sẽ rất lâu tới điểm Global minimum, thậm chí nếu vòng lặp không đủ lớn nó sẽ dừng trước khi đạt tới điểm hội tụ Global minimum.

Đây cũng là lí do mà hàm Cost function cho bài toán Linear Regression là hàm Mean Squared Error. Hàm này đảm bảo yếu tố Convex khi tìm nghiệm tối ưu, hàm Convex sẽ giúp nghiệm bài toán luôn đảm bảo là Global minimum. Ví dụ hình ảnh:

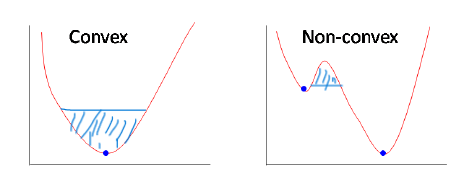
Hình 7: Convex vs Non-convex

Ở Hình 7, phía bên trái là hàm Convex, bên phải không phải hàm Convex. Hiểu đơn giản rằng khi lấy 2 điểm bất kì trên đồ thị và nối chúng lại sẽ được một đường thẳng, nếu đường thẳng này không cắt bất kì điểm nào trên đồ thị nữa sẽ là hàm Convex. Việc tìm ra hàm Convext sẽ giúp ta dễ dàng giải quyết bài toán tối ưu rất nhiều, nghiệm sẽ luôn đảm bảo rằng là Gloabal minimum nếu số vòng lặp phù hợp và learning rate không quá lớn.

4.3. Feature scaling

Trong thực tế, với mỗi loại dữ liệu thì sẽ có kharong giá trị khác nhau, ví dụ: diện tích nhà có thể có giá trị tới hàng trăm, hàng nghìn (mét vuông) tuy nhiên số phòng ngủ thì chỉ có thể là hàng đơn vị (thông thường). Vì vậy khi tiền xử lí dữ liệu, tất cả các thuật toán Machine Learning cần các kiểu dữ liệu về cùng một khoảng nhất định, điều này sẽ giúp máy tính giảm chi phí tính toán rất nhiều và quan trọng nhất là sẽ ảnh hưởng tới performance của thuật toán. Có 2 phương pháp scaling phổ biến nhất giúp đưa các loại dữ liệu về cùng 1 range [0,1] hoặc [-1,1]:

• Min-max scaling [0,1]:

trong đó $x$ là vector dữ liệu ban đầu

• Standard scaling [-1,1]:

trong đó $s_i$ có thể là std (độ lệch chuẩn) hoặc range của $x$ (max - min)

5. Đánh giá và kết luận

• Thuật toán Gradient Descent đã giải quyết được vấn đề về tính toán và bộ nhớ so với cách tính ở bài 1 - Linear Regression

• Tuy nhiên, chọn learning rate và điểm khởi tạo lại chính là điểm yếu của thuật toán này, vì vậy ta phải lựa chọn nhiều lần để có được kết quả mong muốn.

• Gradient Descent là tiền đề của rất nhiều thuật toán tối ưu nâng cao hơn như: Adam, RMSprop, SGD…

• Vì dựa trên đạo hàm nên việc đạo hàm chính xác một hàm số là điều tiên quyết, có 1 cách để debug xem mình đã đạo hàm đúng hay chưa dựa trên định nghĩa của đạo hàm. Tham khảo thêm kiểm tra đạo hàm.

6. Tham khảo

[1] Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow

[2] Week 2 - Machine Learning coursera by Andrew Ng

[3] Bài 7: Gradient Descent (phần 1/2) - Machine Learning cơ bản by Vu Huu Tiep

[4] Gradient descent by Dung Lai