Phụ lục:

• 1. Giới thiệu
• 2. Hàm dự đoán
• 3. Hàm mất mát
• 4. Lập công thức chung
  • 4.1. Hình học
  • 4.2. Đại số tuyến tính
• 5. Thực nghiệm với Python
  • 5.1. Dạng đường thẳng
  • 5.2. Dạng parabol
  • 5.3. Nghiệm bằng thư viện scikit-learn
    • 5.3.1. Dạng đường thẳng
    • 5.3.2. Polynomial Regression
• 6. Đánh giá và kết luận
• 7. Tham khảo

1. Giới thiệu

Hồi quy tuyến tính (Linear Regression) là một thuật toán căn bản nhất đối với bất kì ai bắt đầu học về AI đều sẽ đi qua. Trong thực tế, bài toán hồi quy tuyến tính được ứng dụng rất nhiều vì tính dễ dàng mô tả và dễ dàng triển khai. Hồi quy nói chung là lớp bài toán thuộc học có giám sát (supervised-learning). Dựa trên dữ liệu có sẵn (tức giá trị mục tiêu đã biết) và sự phụ thuộc của giá trị đầu vào để dự đoán một giá trị mới.

Ví dụ đơn giản nhất như: dựa trên diện tích nhà để đưa ra giá dự đoán, dựa trên chiều cao để dự đoán cân nặng,… hoặc rằng buộc thêm như dựa vào diện tích nhà, số phòng, view để đưa ra giá nhà dự đoán.

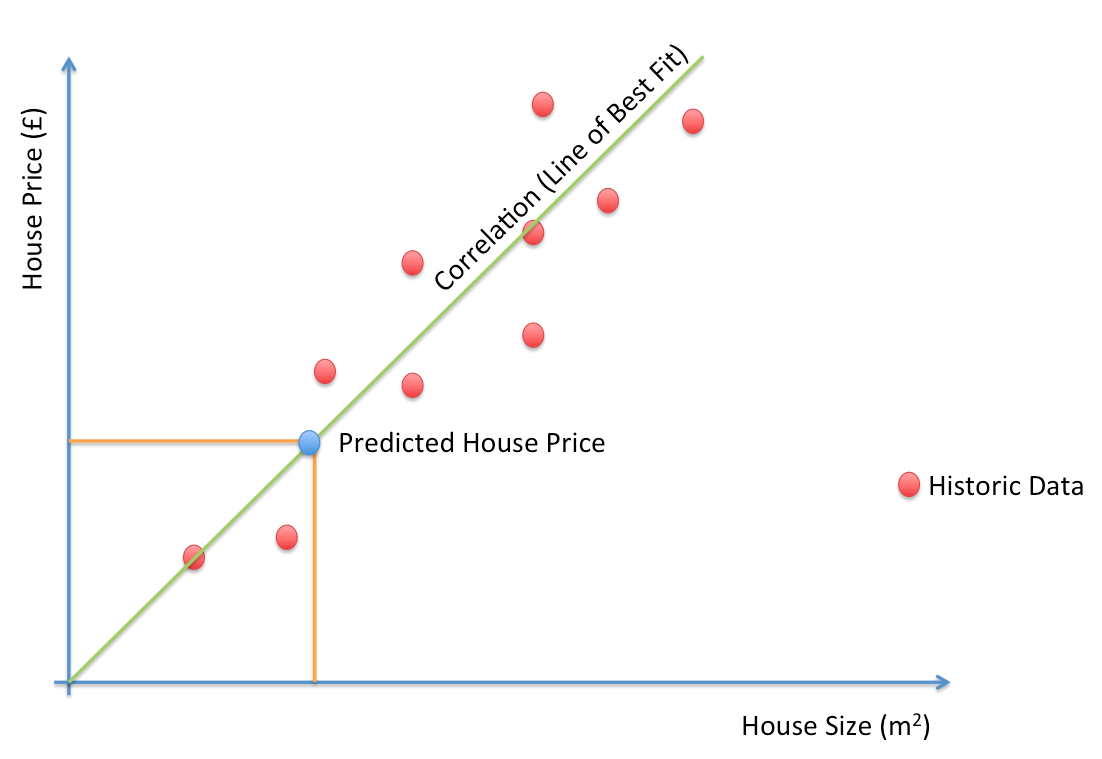
Hình 1: Ví dụ dự đoán giá nhà dựa trên diện tích

2. Hàm dự đoán

Hàm dự đoán hay trong machine learning thường hay gọi là model ám chỉ một hàm số $f$ sẽ là hàm mục tiêu của giá trị cần dự đoán. Một ví dụ đơn giản như dự đoán giá nhà dựa trên số phòng ngủ, diện tích. Vậy đầu vào của bài toán toán sẽ là số phòng ngủ và diện tích, đầu ra sẽ là giá trị dự đoán của căn hộ đó.

Biểu diễn toán học: Cho \(\textbf{r}=[r_1, r_2,...,r_m]\) là vector biểu diễn cho số lượng phòng ngủ mỗi căn hộ lần lượt là \(r_1,r_2,...,r_m\), \(\textbf{s}=[s_1, s_2,...,s_m]\) cũng tương tự \(\textbf{r}\) là vector biểu diễn diện tích. Cuối cùng, \(\textbf{y}=[y_1, y_2,...,y_m]\) là dữ liệu giá mỗi căn hộ đã có sẵn. Các giá trị này đều đã biết trước, mục tiêu của chúng ta là dự đoán xem khi có một căn hộ có \(\textbf{a}\) phòng ngủ, diện tích \(\textbf{b}\) vậy giá căn hộ này là bao nhiêu?

Trong machine learning, ký hiệu \(\hat{y}\) thường dùng để biểu diễn cho một giá trị dự đoán, ta có:

trong đó, \(w_0\) - bias, \(w_1\) và \(w_2\) - trọng số là các giá trị cần tìm, \(r_1\) và \(s_2\) là các giá trị đã biết.

3. Hàm mất mát - Loss function

Khi nhắc đến giá trị dự đoán thì sai số luôn luôn được kèm theo. Sai số tức sự khác biệt giữa giá trị dự đoán và giá trị thực. Sai số càng nhỏ chứng tỏ giá trị dự đoán càng chính xác. Đây cũng là mục tiêu của hàm mất mát nhằm giảm thiểu sai số tối đa nhất có thể.

Loss function chỉ sai số của một điểm dữ liệu còn cost function sẽ chỉ ra trung bình sai số trên toàn tập dữ liệu. Đây là những thuật ngữ cơ bản và rất quan trọng trong machine learning. Thường các thuật toán tối ưu sẽ tối ưu phần này và cũng là phần tối ưu khó nhất vì yêu cầu kiến thức toán lớn.

Giả sử \(f\) là giá trị thực của một căn hộ, \(f'\) là giá trị dự đoán và \(e\) là sai số khi dự đoán. Điều ta mong muốn là làm sao cho phương trình sau xảy ra:

Và trong bài toán hồi quy tuyến tính (Linear Regression) chúng ta cần tối ưu sao cho \(e\) có giá trị nhỏ nhất có thể. Phương trình cần tối ưu trong bài toán:

4. Lập công thức chung

Với bài toán dự đoán giá nhà dựa trên diện tích, ta có:

Hàm dự đoán:

trong đó \(x_i\) biểu diễn giá trị diện tích, \(\hat{y_i}\) biểu diễn giá trị dự đoán tương ứng của mẫu dữ liệu thứ $i$, $w_0$ và $w_1$ là trọng số cần tìm

Hàm mất mát:

trong đó $m$ là số lượng dữ liệu, $y_i$ là giá trị thực của mẫu dữ liệu thứ $i$.

Lúc này khi đã định nghĩa được 2 hàm số trên, chúng ta có thể đi tìm nghiệm cho bài toán tức tìm $w_0$ và $w_1$. Với thuật toán này, có nhiều phương pháp để tìm nghiệm. Các phương pháp dựa trên toán hình học, đại số tuyến tính và giải tích. Trong bài này, mình sẽ trình bày 2 phương pháp: hình học và đại số tuyến tính.

4.1. Hình học

Cho 3 điểm dữ liệu $A(x_1,y_1)$, $B(x_2,y_2)$, $C(x_3,y_3)$ và đường màu xanh chính là đường thẳng ta cần tìm, ta có:

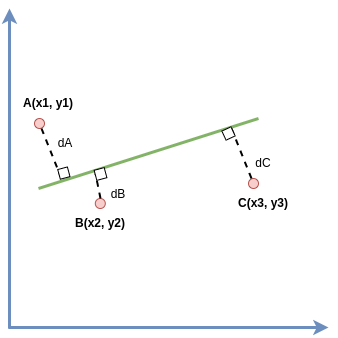
Giả sử đường thẳng màu xanh đi qua 3 điểm A,B,C thì ta có 3 phương 2 ẩn $w_0$ và $w_1$:

Nhưng với 3 phương trình 2 ẩn thì việc tìm nghiệm chính xác là điều không thể, vì vậy ta sẽ đi tìm $w_0$ và $w_1$ gần đúng sao cho sai số là bé nhất từ đó các nhà toán học đã đưa ra một giá trị cần tối ưu: $d_A^{2} + d_B^{2} + d_C^{2}$ bé nhất.

Từ (1), (2), (3) ta có thể vector hóa dưới dạng: \(\begin{bmatrix}y_1\\ y_2 \\ y_3\end{bmatrix} \approx w_0\begin{bmatrix}1\\ 1 \\ 1\end{bmatrix} + w_1\begin{bmatrix}x_1\\ x_2 \\ x_3\end{bmatrix} (4)\). Đặt \(y = \begin{bmatrix}y_1\\ y_2 \\ y_3\end{bmatrix}\), \(o = \begin{bmatrix}1\\ 1 \\ 1\end{bmatrix}\),\(x = \begin{bmatrix}x_1\\ x_2 \\ x_3\end{bmatrix}\). Lúc này biểu diễn dưới dạng hình học ta sẽ được

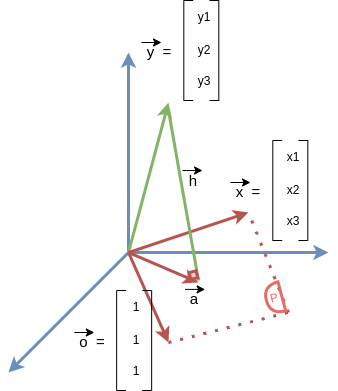
Với những giá trị khác nhau của $w_0$ và $w_1$ ta sẽ thu được mặt phẳng $\textbf{(P)}$, vế phải của phương trình (4) sẽ tạo được một vector $\textbf{a}$ nằm trong mặt phẳng $\textbf{(P)}$. Do đó, ta cần tìm $w_0$ và $w_1$ để $\textbf{y}$ và $\textbf{a}$ gần nhau nhất. Để điều kiện này xảy ra khi và chỉ khi $\textbf{a}$ chính là hình chiếu của $\textbf{y}$ lên mặt phẳng $\textbf{(P)}$, gọi vector hình chiếu đó là $\textbf{h}$.

Lúc này ta có $\textbf{h}$ $\bot$ $\textbf{x}$ và $\textbf{h}$ $\bot$ $\textbf{o}$ (tính chất của đường thẳng vuông góc mặt phẳng) $=>$ $\textbf{x}^T.\textbf{h}=0$ và $\textbf{o}^T.\textbf{h}=0 (5)$

Đặt \(W = \begin{bmatrix}w_0\\ w_1 \end{bmatrix}\) và \(X = \begin{bmatrix}1 && x_1 \\ 1 && x_2 \\ 1 && x_3 \end{bmatrix}\), theo (5) thì ta được $X^T.\textbf{h}=0$ mà $\textbf{h}$ = $\textbf{y} - \textbf{a}$ (tính chất cộng vector)

Lại có $\textbf{a} = X.W => X^T.\textbf{y} = X^T.X.W => W = (X^T.X)^{-1}.X^T.\textbf{y}$ (Lưu ý: dấu . biểu diễn dot product).

Tới đây chúng ta đã tìm được W là vector chứa 2 giá trị $w_0$ và $w_1$.

4.2. Đại số tuyến tính

Để cho dễ dàng triển khai code ở phần sau, thì bắt đầu từ phần này các dữ liệu sẽ được vector và ma trận hóa. Vì vậy các công thức liên quan cũng sẽ cho ra vector hoặc ma trận.

Cho $m$ mẫu dữ liệu đã có nhãn về giá trị diện tích và giá trị căn hộ.

Để tìm nghiệm tối ưu bài toán, ta sẽ đạo hàm hàm J để tìm cực tiểu

Ta thấy nghiệm giải bằng phương pháp sử dụng đại số tuyến tính kết hợp đạo hàm cho ra nghiệm bài toán giống với phương pháp hình học trên. Phương pháp sử dụng đạo hàm này có thể mở rộng ra các thuật toán tối ưu trong machine learning như Gradient Descent.

5. Thực nghiệm với Python

5.1. Dạng đường thẳng

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import numpy as np # đstt
import matplotlib.pyplot as plt # visualize

# Dữ liệu
X = np.array([[2,5,7,9,11,16,19,23,22,29,29,35,37,40,46]]).T
Y = np.array([[2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]]).T

# Visualize dữ liệu
plt.scatter(X, Y)

# thêm vector cột 1 vào dữ liệu input
m = X.shape[0]
ones = np.ones((m,1), dtype=np.int8)
X = np.concatenate((ones,X), axis=1)

# tìm nghiệm W cho bài toán
W = np.linalg.inv(X.T.dot(X)).dot(X.T.dot(Y))
w0,w1 = W[0][0],W[1][0]

# lấy điểm đầu và điểm cuối 
# để vẽ đường thẳng cần tìm
x0 = np.linspace(2,46,2)
y0 = w0 + w1*x0

# visualize đường thẳng cần tìm
plt.plot(x0,y0,'r')
plt.xlabel('Diện tích')
plt.ylabel('Giá nhà')
plt.show()

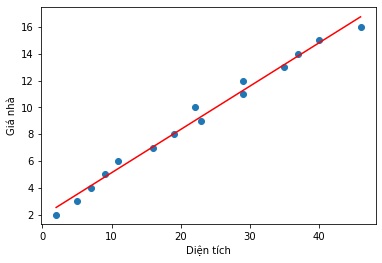
Hình 2: Visualize đường thẳng cần tìm

Và giá trị nghiệm W ta tìm được là:

1
2
3
print(W)
>>> [[1.88039364]
     [0.32361847]]

5.2. Dạng Parabol

Khác một chút so với dữ liệu dạng đường thẳng, nếu dữ liệu dạng không đơn điệu thì hàm dự đoán của ta cần thay đổi một chút. Ví dụ với hàm parabol đã quen thuộc khi còn học cấp 3: $y = ax^2 + bx + c$. Do vậy ở bài toán với hàm dự đoán là parabol, ta cần tìm 3 nghiệm $w_0, w_1$ và $w_2$.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import numpy as np # đstt
import matplotlib.pyplot as plt # visualize

# Dữ liệu
X = np.array([[2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]]).T
Y = np.array([[2,5,7,9,11,16,19,23,22,29,29,35,37,40,46,42,39,31,30,28,20,15,10,6]]).T

# Visualize dữ liệu
plt.scatter(X, Y)

# thêm vector cột 1 vào dữ liệu input
m = X.shape[0]
ones = np.ones((m,1), dtype=np.int8)
X_square = np.square(X)
X = np.concatenate((ones,X), axis=1)
X = np.concatenate((X,X_square),axis=1)

# tìm nghiệm W cho bài toán
W = np.linalg.inv(X.T.dot(X)).dot(X.T.dot(Y))
w0,w1,w2 = W[0][0],W[1][0],W[2][0]

# lấy 10000 điểm để vẽ 
# để vẽ đường thẳng cần tìm
x0 = np.linspace(2,25,10000)
y0 = w0 + w1*x0 + w2*(x0**2)

# visualize đường thẳng cần tìm
plt.plot(x0,y0,'r')
plt.xlabel('Diện tích')
plt.ylabel('Giá nhà')
plt.show()

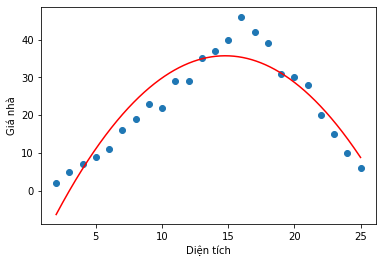
Hình 3: Visualize parabol cần tìm

Và giá trị nghiệm W ta tìm được ta:

1
2
3
4
print(W)
>>>	[[-20.44709486]
	[  7.60002888]
	[ -0.25718303]]

5.3. Nghiệm bằng thư viện scikit-learn

Ở phần này ta sẽ sử dụng thư viện scikit-learn để thực hành bài toán và so sánh xem giữa nghiệm bài toán tự implement và nghiệm của bài toán được xử lí bởi thư viện có mang tới kết quả giống nhau không. scikit-learn là một trong những thư viện rất phổ biến để thực hành các mô hình Machine Learning cơ bản, ngoài ra trong scikit-learn sẽ gồm rất nhiều thư viện tiện ích như dataset, parameters tuning strategy,…

5.3.1. Dạng đường thẳng

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from sklearn.linear_model import LinearRegression
import numpy as np

# Dữ liệu
X = np.array([[2,5,7,9,11,16,19,23,22,29,29,35,37,40,46]]).T
Y = np.array([[2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]]).T

# Khởi tạo model
lin_reg = LinearRegression()

# Fit/train model
lin_reg.fit(X, Y)

print('W = {}, b = {}'.format(lin_reg.coef_,lin_reg.intercept_))

Kết quả thu được là:

1
W = [[0.32361847]], b = [1.88039364]

Ta thấy kết quả nghiệm của bài toán giữa phương pháp tự thực hiện ở phần 5.1 và thư viện scikit-learn đã đưa ra kết quả giống nhau. Sau khi tìm được nghiệm bài toán, việc tiếp theo khi có dữ liệu cần dự đoán bạn chỉ cần gọi tới hàm predict để lấy ra giá trị dự đoán.

5.3.2. Polynomial Regression

Ở phần 5.2 dữ liệu lúc này không còn ở dạng tuyến tính, tuy nhiên chúng ta vẫn có thể sử dụng mô hình tuyến tính để tìm nghiệm tối ưu. Ở phần 5.2 mình đã sử dụng cách thêm 1 biến bình phương để giúp mô hình có thể khái quát hóa dữ liệu tốt hơn. Vì vậy, trong scikit-learn cũng sẽ cung cấp một class PolynomialFeatures giúp thay đổi giữ liệu gốc ban đầu thành dữ liệu có cả bậc mũ cao hơn.

Đầu tiên sẽ là bước tiền xử lí cho bài toán:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
import numpy as np # đstt
import matplotlib.pyplot as plt # visualize

# Dữ liệu
X = np.array([[2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]]).T
Y = np.array([[2,5,7,9,11,16,19,23,22,29,29,35,37,40,46,42,39,31,30,28,20,15,10,6]]).T

# Visualize dữ liệu
plt.scatter(X, Y)

poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)

Kết quả của X ban đầu và X_poly sau khi sử dụng PolynomialFeatures với mũ bậc 2:

1
2
3
4
print(X[0])
print(X_poly[0])
>>> [2]
    [2. 4.]

Việc tiền xử lí này đã giúp mô hình của ta có thêm 1 biến bậc cao, bước tiếp theo chỉ cần khai báo mô hình và fit tương tự ở phần trên:

1
2
lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)

Kết quả chính xác với hàm implement ở trên:

1
2
print('b = {}, W = {}'.format(lin_reg.intercept_, lin_reg.coef_))
>>> b = [-20.44709486], W = [[ 7.60002888 -0.25718303]]

6. Đánh giá và kết luận

• Nếu bài toán có dữ liệu dạng parabol mà vẫn sử dụng hàm dự đoán là đường thẳng thì sao? Vẫn được, nhưng sai số cao, chưa thể tối ưu bằng sử dụng hàm parabol. Giả sử, đầu vào lúc này không phải là 1 chiều mà là 2 chiều thì hàm dự đoán sẽ trở thành một mặt phẳng và công thức nghiệm trên vẫn đúng. Còn đầu vào có quá nhiều chiều dữ liệu thì lúc này mô hình của bài toán sẽ là một siêu phẳng (hyper plan). Như vậy bài toán dự đoán của chúng ta đã được giải quyết bằng cách tìm nghiệm W. Để dự đoán một điểm mới ta chỉ cần áp dụng như tính y0 ở trên.

• Việc tìm ma trận nghịch đảo là điểm yếu của cách làm này vì sẽ tốn thêm time complexity ($O(n^{2.4}) - O(n^{3})$ với $n$ là số lượng features của bài toán) và space complexity . Vì vậy, trong thư viện scikit-learn các nhà phát triển đã tối ưu phương pháp giải bằng ứng dụng của thuật toán SVD - Singular Value Decomposite và đạt được tốc độ khoảng $O(n^2)$. Tuy nhiên, cả 2 phương pháp này sẽ rất chậm với những bộ dữ liệu có features cao chiều (100.000) nên sẽ phù hợp hơn với những bộ dữ liệu thấp chiều (kể cả nhiều dữ liệu) thì phương pháp này vẫn sẽ hoạt động tốt.

• Ở hàm mất mát, có một số thuật toán nhằm tránh overfiting như Ridge Regression, Lasso Regression hay trong deep learning là regurlization.

• Thuật toán này sử dụng trung bình tổng sai số của giá trị dự đoán và giá trị thật để triển khai và đánh giá, vì vậy khi tồn tại dữ liệu “nhiễu” sẽ gây ảnh hưởng tới chất lượng dự đoán. Một số phương pháp khắc phục đó là sử dụng: MAE Loss, Huber Loss… Nhưng vì các hàm này khá khó để giải trực tiếp vì vậy, thường sẽ loại bỏ các dữ liệu “nhiễu” trước khi traning.

7. Tham khảo

[1] Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow

[2] Week 2 - Machine Learning coursera by Andrew Ng

[2] Bài 3: Linear Regression - Machine Learning cơ bản by Vu Huu Tiep

[3] Linear Regression by Dung Lai