7. K-means
21 Nov 2021Phụ lục:
- 1. Giới thiệu
- 2. Kết quả mong muốn
- 3. Hàm mất mát
- 4. Các bước giải bài toán
- 5. Thực nghiệm với Python
- 6. Cải tiến K-means
- 7. Đánh giá và kết luận
- 8. Tham khảo
1. Giới thiệu
Trong thực tế, những bài toán như dự báo, phân loại yêu cầu phần lớn dữ liệu cần phải gán nhãn. Vậy nếu khi có một tập dữ liệu về khách hàng như: sở thích, thói quen, giới tính, độ tuổi… làm sao để phân loại khách hàng nào là tiềm năng hoặc không trong khi các dữ liệu chưa được gán nhãn. Việc đi tìm nhãn cho khách hàng (dữ liệu) chính là mục tiêu của thuật toán K-means. Và sau khi gán nhãn cho khách hàng thành công, khi một khách hàng mới đến ta có thể trả lời rằng người này thuộc nhóm khách hàng tiềm năng hay không, từ đó có thể phát triển rất nhiều chiến lược về khuyến mại và marketing.
Khác với các bài toán thuộc học có giám sát (supervised-learning) - các biến mục tiêu đã biết, K-means là lớp bài toán thuộc học không giám sát (unsupervised-learning) - các biến mục tiêu chưa biết.
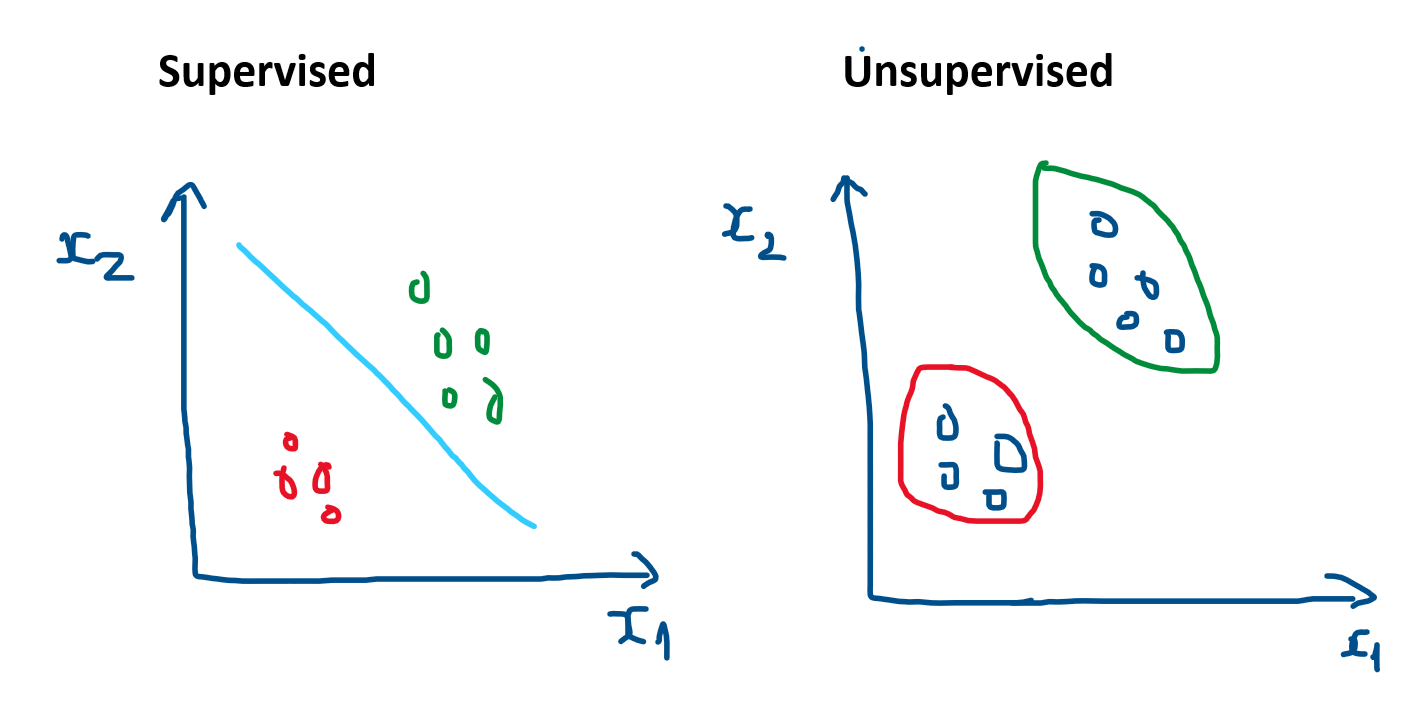
Hình 1: Supervised vs Unsupervised
2. Kết quả mong muốn
Trong thuật toán K-means, với tập dữ liệu có $m$ samples. Ta cần phân nhóm $m$ samples thành $k$ $(k < m)$ cụm, với mỗi cụm sẽ có độ tương đồng về dữ liệu nhất định (có thể là sở thích, tích cách, giới tính… đối với người). Với hình 1 bên phải, tức ta cần phân nhóm 9 samples thành 2 cụm: màu xanh lục và màu đỏ.
Ví dụ với tập dữ liệu 2 chiều sau:
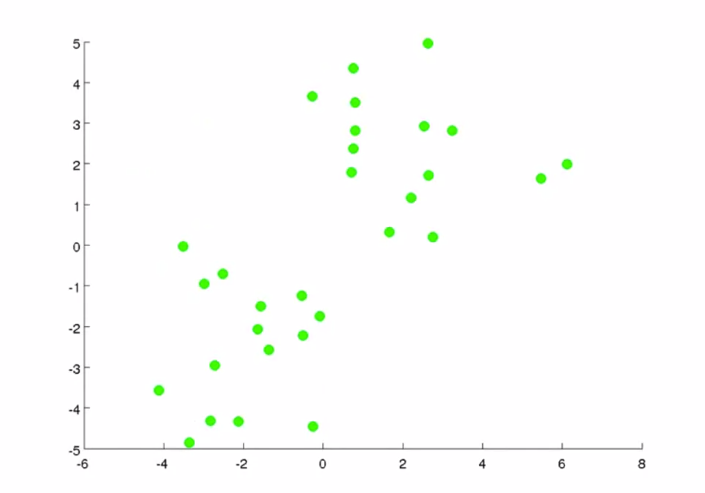
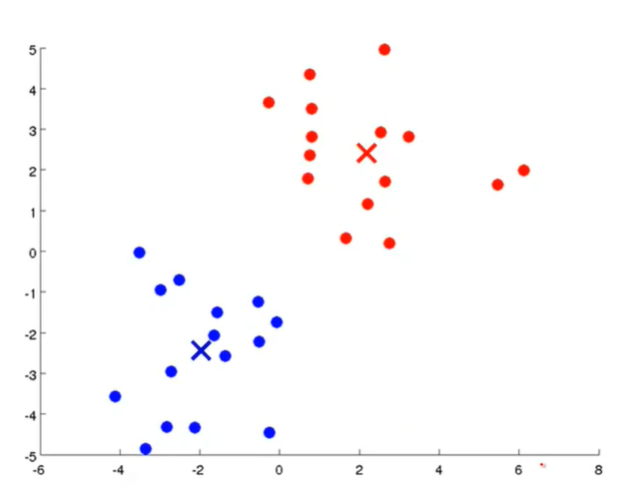
Hình 2: Hình trái - Dataset, Hình phải - Kết quả (Nguồn: Machine learning - Coursera)
Với input là tập dataset chưa hề có nhãn cho từng điểm dữ liệu, mong muốn của bài toán nhằm gán nhãn cho toàn bộ dữ liệu. Bằng trực giác ta có thể thấy rằng với Hình 2 - bên phải biểu thị kết quả rằng những điểm dữ liệu có khoảng cách càng gần nhau sẽ có màu càng giống nhau. Tuy nhiên, làm sao mà kết quả có thể chia làm 2 màu xanh, đỏ rõ ràng như vậy? Đây chính là mấu chốt của thuật toán này, nếu để ý 2 điểm ‘x’ màu đỏ và xanh có ở kết quả thì ban đầu dữ liệu không hề có 2 điểm này. Hơn nữa, nếu gióng tọa độ của 2 điểm này lên trục tọa độ ta sẽ thấy giá trị tọa độ của nó là trung bình cộng của toàn bộ điểm dữ liệu thuộc màu của nó. 2 điểm này chính là tâm cụm (centroids) của mỗi màu dữ liệu.
Giả sử rằng mỗi điểm dữ liệu chỉ thuộc vào đúng một nhóm, trong thuật toán K-means, ta cần lựa chọn số lượng cụm như là hyper-parameter đầu vào. Với hình trên thì ta có thể thấy số lượng cụm là 2 khá hợp lí. Vì vậy, từ dữ liệu đầu vào và số lượng nhóm chúng ta muốn tìm, hãy chỉ ra centroids (điểm trung tâm cụm) của mỗi nhóm và phân các điểm dữ liệu vào các nhóm tương ứng.
3. Hàm mất mát
Giả sử ta có $m$ điểm dữ liệu. $\mathbf{X} = \begin{bmatrix} x^{(1)}, x^{(2)}, x^{(3)},…x^{(m)} \end{bmatrix}$ trong đó $x^{(i)} \in \mathbb{R}^d $, $i$ chạy từ 1,2,…$m$, $\mathbf{X} \in \mathbb{R}^{d \times m}$. Có $K$ cụm với $K < m$. Đặt $c_k$ là tâm cụm ta đã tìm được và $x^{(i)}$ là điểm dữ liệu thuộc cụm này. Điều ta mong muốn là khoảng cách (sai số) giữa $c_k$ và $x_i$ là nhỏ nhất có thể. Và sai số trên toàn tập dữ liệu là:
\[J = \sum_{j=1}^K\sum_{i=1}^m \|\mathbf{x}^{(i)} \in j - \mathbf{c}_j\|_2^2\]Ở công thức trên ta hiểu là: tổng sai số bằng tổng khoảng cách của tâm cụm $j$ với các điểm dữ liệu $x_i$ thuộc cụm $j$. Trong đó $j$ được hiểu ngầm là nhãn cho dữ liệu vì vậy ta sẽ có $K$ nhãn khác nhau. Và $c_j$ là trung bình cộng của các điểm thuộc cụm $j$.
Ở đây, mình đã đơn giản hóa cách biểu diễn để khi thực code sẽ dễ dàng hơn, bạn có thể đọc thêm tại đây để xem cách biểu diễn dạng vector one-hot, chứng minh tâm cụm là trung bình cộng của các điểm dữ liệu thuộc cụm đó và hàm Loss luôn giảm sau mỗi vòng lặp. Ngoài ra thuật toán sẽ dừng sau 1 số hữu hạn vòng lặp.
4. Các bước giải bài toán
-
Bước 1: Chọn $K$ điểm dữ liệu làm điểm tâm cụm ban đầu.
-
Bước 2: Tính khoảng cách mỗi điểm dữ liệu với tâm cụm và gán dữ liệu vào cụm gần nhất.
-
Bước 3: Nếu việc gán dữ liệu vào từng cluster ở bước 2 không thay đổi so với vòng lặp trước nó thì ta dừng thuật toán.
-
Bước 4: Cập nhật điểm tâm cụm bằng trung bình cộng các dữ liệu thuộc cụm đó.
-
Bước 5: Quay lại bước 2.
5. Thực nghiệm với Python
5.1. Implement thuật toán
Đầu tiên ta sẽ tạo dataset, tuy nhiên lưu ý 2 biến true_centroids và true_labels trong thực tế sẽ không có.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import numpy as np # ĐSTT
import random
import matplotlib.pyplot as plt # Visualize
from sklearn.datasets import make_blobs # Make the dataset
# Init original centroids
true_centroids = [[1, 1], [-1, -1], [1, -1]]
# dataset
X, true_labels = make_blobs(n_samples=750, centers=true_centroids,
cluster_std=0.4, random_state=0)
# predict labels
labels = []
# Visualize dữ liệu
plt.plot(X[:,0],X[:,1],'o')
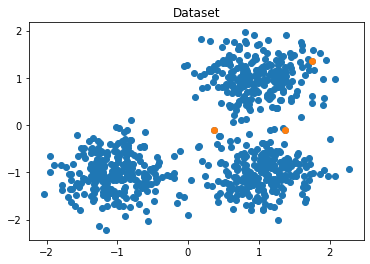
plt.title('Dataset')
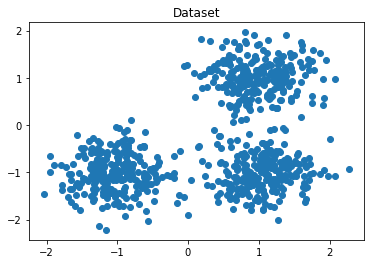
Hình 3: Visualize dataset
Giả sử với bộ dữ liệu trên, ta khởi tạo K = 3 là số cụm và sẽ thu các tâm cụm tương ứng với giá trị ngẫu nhiên.
1
2
3
4
5
6
7
8
9
10
11
12
13
# Init random centroids
def init_centroids(K):
centroids = []
K = 3
for i in range(K):
x = random.sample(list(X), 1)
centroids.append(x[0])
centroids = np.array(centroids)
return centroids
K = 3
centroids = init_centroids(K)
plt.plot(centroids[:,0],centroids[:,1],'o')
Hình 4: Khởi tạo tâm cụm
Tiếp theo là hàm tính toán khoảng cách giữa 2 điểm với K-means khoảng cách được sử dụng sẽ là norm 2.
1
2
3
# Tính khoảng cách 2 điểm
def distance(p1,p2):
return np.linalg.norm(p1-p2,2)
Tiếp theo ta cần tính toán khoảng cách của từng điểm dữ liệu với từng centroids, khoảng cách ngắn nhất của điểm dữ liệu với từng centroids sẽ được coi là nhãn của điểm dữ liệu đó.
1
2
3
4
5
6
7
8
9
10
11
12
13
# Update labels for dataset
def update_labels(X):
labels = []
for i in range(len(X)):
fake_distance = 999999
label = -1
for j in range(len(clusters)):
d = distance(X[i],clusters[j])
if d < fake_distance:
fake_distance = d
label = j
labels.append(label)
return labels
Sau khi đã lấy nhãn cho toàn bộ dữ liệu, ta cần cập nhật giá trị tâm cụm bằng cách tính trung bình cộng của những điểm dữ liệu thuộc nhãn của cụm.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Update centroids
def update_centroids(centroids, X, labels):
before_centroids = centroids.copy()
for i in range(len(centroids)):
count = 0
x0 = 0
y0 = 0
for j in range(len(X)):
if i == labels[j]:
count += 1
x0 += X[j][0]
y0 += X[j][1]
if count == 0:
break
x0 /= count
y0 /= count
centroids[i][0] = x0
centroids[i][1] = y0
return centroids, before_centroids
Cuối cùng là điều kiện dừng của thuật toán, ở đây ta sét cho tới khi giá trị của centroids không đổi thì sẽ dừng.
1
2
3
4
# When stop
def stop(centroids,new_centroids):
return (set([tuple(a) for a in centroids]) ==
set([tuple(a) for a in new_centroids]))
Các hàm quan trọng của bài toán đã được hoàn thành, bây giờ ta cần lắp ghép chúng vào theo phần 4 để tìm nghiệm cho bài toán.
1
2
3
4
5
6
7
while True:
labels = update_labels(X)
centroids, before_centroids = update_centroids(centroids, X, labels)
if stop(centroids, before_centroids):
break
plt.scatter(X[:,0], X[:,1], c = labels, cmap='rainbow')
plt.scatter(centroids[:,0], centroids[:,1], color='black')
Kết quả:
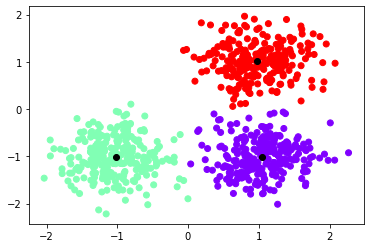
Hình 5: Kết quả thu được
Nhận xét:
-
Sau 1 số vòng lặp, ta đã chia được dữ liệu thành 3 cụm khác nhau trông có vẻ được phân thành 3 nhóm khá rõ ràng.
-
Lúc này khi có điểm dữ liệu mới đến, ta chỉ cần tính toán khoảng cách giữa điểm đó với các tâm cụm để lấy ra khoảng cách nhỏ nhất chính là thuộc cụm đó. Phần này khá dễ, bạn có thể thử implement.
5.2. Nghiệm bằng thư viện scikit-learn
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from sklearn.cluster import KMeans
import matplotlib.pyplot as plt # Visualize
from sklearn.datasets import make_blobs # Make the dataset
# Init original centroids
true_centroids = [[1, 1], [-1, -1], [1, -1]]
# dataset
X, true_labels = make_blobs(n_samples=750, centers=true_centroids,
cluster_std=0.4, random_state=0)
k = 3
kmeans = KMeans(n_clusters = k)
kmeans.fit(X)
centroids = kmeans.cluster_centers_
labels = kmeans.predict(X)
plt.scatter(X[:,0], X[:,1], c = labels, cmap='rainbow')
plt.scatter(centroids[:,0], centroids[:,1], color='black')
Kết quả:
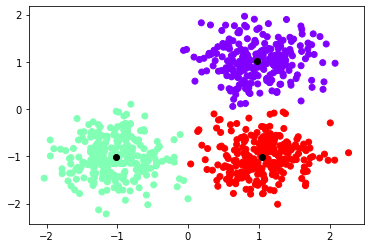
Hình 6: Kết quả thu được
Nhận xét:
-
Kết quả thu được của scikit-learn giống với hàm mà mình đã implement, các giá trị centroids và nhãn đã giống nhau.
-
Với scikit-learn, khi có dữ liệu mới ta chỉ cần gọi hàm
predictđể dự đoán xem điểm đó thuộc cụm nào (chú ý hàm này có thể dùng để dự đoán không chỉ một mà có thể là tập hợp các điểm dữ liệu). Ta nhận thấy rằng tuy thuật toán chạy quá trình training có thể mất thời gian một chút ($O(mkn)$) với $m$ là số lần lặp của thuật toán và $n$ là số lượng samples, nhưng khi dự đoán thì chỉ mất ($O(k)$) với $k$ là số lượng cụm. -
Tuy nhiên, một điểm yếu của K-means là việc random các điểm centroids ban đầu sẽ ảnh hưởng tới kết quả của bài toán. Như ở phần implement 5.1, mình đã thử chạy vài lần ở mỗi lần số lượng vòng lặp sẽ khác nhau phụ thuộc vào điểm khởi tạo ban đầu thậm chí đôi khi nghiệm cuối cùng thu được không phải là nghiệm tối ưu của bài toán (local optima), bằng trực giác ta thấy rằng các điểm khởi tạo ban đầu có khoảng cách càng xa nhau càng tốt. Ví dụ minh họa:
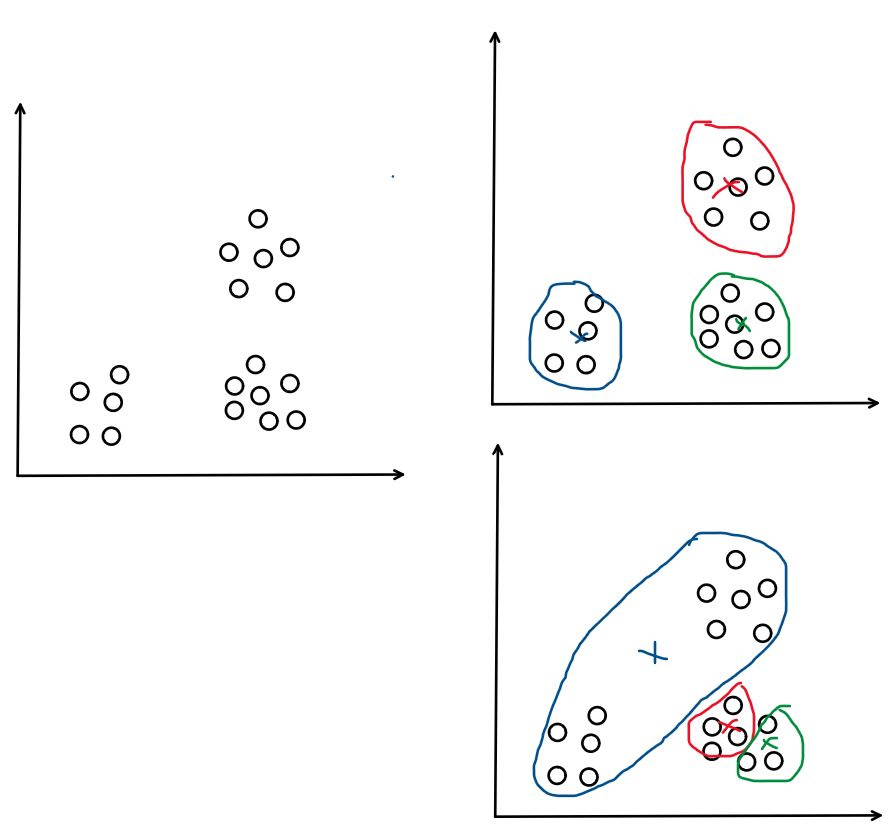
Hình 7: Điểm yếu của khởi tạo
-
Ngoài ra số lượng cụm cũng cần phải khởi tạo ban đầu, với bộ dữ liệu 2D ở trên thì khá dễ để chọn nhưng trong trường hợp dữ liệu ở dạng cao chiều sẽ không thể nhìn trực tiếp để chọn số lượng cụm. Vì vậy phần tiếp theo mình sẽ giới thiệu 1 số cách cải tiến những vấn đề này.
-
Tất nhiên rằng trong thư viện scikit-learn, những điểm yếu về khởi tạo đã được tối ưu bằng thuật toán K-means++ thay vì thuật toán gốc, nếu tò mò bạn có thể đọc tiếp phần 6 để xem cách cải tiến thuật toán K-means gốc.
6. Cải tiến K-means
Ở phần này ta sẽ xem xét 2 vấn đề yếu điểm của K-means đó là những điểm centroids khởi tạo ban đầu và số lượng cụm. Một số hướng giải quyết cũng sẽ được trình bày.
6.1. Khởi tạo
Như đã đề cập bên trên, vấn đề khởi tạo những centroids ban đầu sẽ ảnh hưởng tới kết quả của bài toán (hội tụ tới local optima hay global optima). Vì vậy nếu có cách nào đó chọn lựa những điểm khởi tạo ‘tốt’ một chút sẽ giúp bài toán cải tiến nhiều về performance.
6.1.1. Thử sai
Có một điều chắc chắn rằng nếu nghiệm cuối cùng của bài toán (global optima) sẽ đưa ra hàm cost function đạt giá trị nhỏ nhất. Vì vậy, ta có thể sử dụng một cách ‘mò’ đó là đưa ra giới hạn số hạn $m$ vòng lặp, ở mỗi vòng lặp ta sẽ khởi tạo tâm cụm ngẫu nhiên và tính toán cập nhật tâm cụm như bình thường.Tuy nhiên, ta sẽ tính thêm hàm cost function và lấy ra giá trị hàm cost function có giá trị nhỏ nhất trong $m$ lần lặp và coi đây là nghiệm tối ưu cuối cùng của bài toán.
Đầu tiên là hàm cost function của thuật toán K-means:
1
2
3
4
5
6
7
# Hàm này sẽ tính tổng khoảng cách trong mỗi cụm
# Và kết quả đầu ra ta mong muốn hàm này có giá trị nhỏ nhất
def cost_function(centroids, X, labels):
cost_f = 0
for i in range(len(X)):
cost_f += distance(centroids[labels[i]], X[i])
return cost_f
Tiếp theo ta sẽ thay vòng lặp while: True bên trên bằng đoạn code sau:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
final_centroids = []
final_labels = []
cost = 9999999
for i in range(500):
K = 3
centroids = init_centroids(K)
labels = update_labels(X)
labels, centroids, _ = update_centroids(centroids, X, labels)
labels, centroids = np.array(labels), np.array(centroids)
cost_f = cost_function(centroids, X, labels)
if cost_f < cost:
cost = cost_f
final_centroids = centroids
final_labels = labels
plt.scatter(X[:,0], X[:,1], c = final_labels, cmap='rainbow')
plt.scatter(final_centroids[:,0], final_centroids[:,1], color='black')
Kết quả:
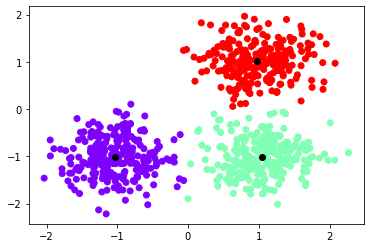
Hình 8: Kết quả phương pháp thử sai
Nhận xét:
-
Với phương pháp này thì ta có thể đảm bảo chắc chắn rằng kết quả cuối cùng của thuật toán sẽ là nghiệm tối ưu của bài toán và đây cũng là cách mà thư viện scikit-learn làm việc với thuật toán K-means (lấy hàm cost có giá trị nhỏ nhất làm nghiệm cuối cùng) với 10 lần lặp.
-
Mặc dù phương pháp này sẽ mất time khá nhiều vì sẽ lựa từ đầu rất nhiều lần mỗi lần như vậy lại lặp lại thuật toán nhưng như đã đề cập bên trên khi đã train/fit được rồi thì việc dự đoán sẽ rất nhanh.
6.1.2. K-means++
Bằng trực giác ta có thể cảm nhận rằng, các điểm khởi tạo ban đầu đôi một có khoảng cách càng xa nhau càng tốt. Nó sẽ rất tiện lợi cho việc cập nhật tâm cụm hơn nữa nó sẽ giúp tránh những trường hợp bị rơi vào nghiệm (local optima) như ở hình 7. Từ đây, thuật toán K-means++ ra đời nhằm giải quyết vấn đề về khởi tạo này và các bước cập nhật/tính toán còn lại vẫn như cũ.
Các bước khởi tạo như sau, giả sử có $K$ cụm:
-
Bước 1: Chọn 1 centroid ngẫu nhiên từ dữ liệu ban đầu.
-
Bước 2: Mỗi điểm dữ liệu ta sẽ tìm khoảng cách với các tâm cụm đang có và chọn ra khoảng cách ngắn nhất và được một tập hợp khoảng cách gọi là
dists. -
Bước 3: Từ tập hợp
distschọn raindexcủa khoảng cách lớn nhất. -
Bước 4: Tâm cụm mới chính là giá trị của
indextrong dữ liệu ban đầu. -
Bước 5: Lặp lại bước 2, 3, 4 cho tới khi hết $K - 1$ lần.
Thao tác với Python:
Các hàm và dataset đã được implement bên trên nên mình sẽ không sử dụng lại ở phần code này vì hơi dài.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# Hàm để vẽ các bước chọn tâm cụm
def plot(data, centroids):
plt.scatter(data[:, 0], data[:, 1], marker = '.',
color = 'gray', label = 'data points')
plt.scatter(centroids[:-1, 0], centroids[:-1, 1],
color = 'black', label = 'previously centroids')
plt.scatter(centroids[-1, 0], centroids[-1, 1],
color = 'red', label = 'next centroid')
plt.title('Selected % d th centroid'%(centroids.shape[0]))
plt.legend()
plt.show()
# Thuật toán khởi tạo
def initialize(data, K):
centroids = []
# chọn ngẫu nhiên tâm cụm đầu tiên (bước 1)
random_idx = np.random.randint(data.shape[0])
centroids.append(data[random_idx])
plot(data, np.array(centroids))
for k in range(K - 1):
dists = []
# Bước 2
# tìm khoảng cách của mỗi điểm dữ liệu với các tâm cụm đang có
# chọn ra khoảng cách ngắn nhất
for i in range(data.shape[0]):
point = data[i, :]
d = 999999
for j in range(len(centroids)):
temp_dist = distance(point, centroids[j])
d = min(d, temp_dist)
dists.append(d)
dists = np.array(dists)
# Bước 3
# lấy ra index có giá trị lớn nhất trong dists
next_centroid = data[np.argmax(dists), :]
# Bước 4
# Tâm cụm mới chính là giá trị của index trong dữ liệu ban đầu
centroids.append(next_centroid)
plot(data, np.array(centroids))
return centroids
initialize(X,3)
Kết quả:
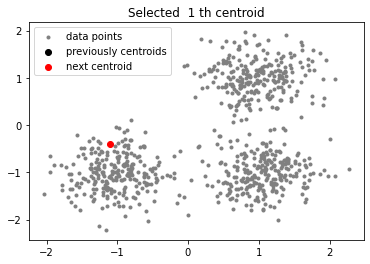
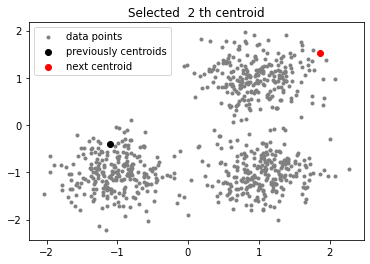
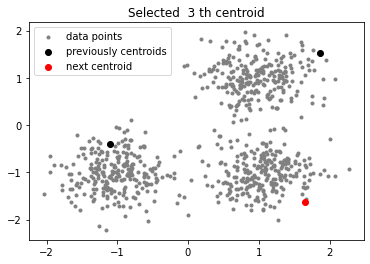
Giải thích:
Chắc hẳn khi đọc tới đây bạn sẽ chưa hiểu tại sao các bước như trên lại có thể tìm ra được tâm cụm mới giúp cải tiến thuật toán. Lúc đầu mình đọc cũng vậy, hơi khó hiểu về mặt số học và cách giải thích tại sao các bước này có thể làm được. Tuy nhiên, khi vẽ các bước lên mặt phẳn 2D bạn sẽ thấy cái hay của phương pháp này. Ở bước 2 và bước 3 chính là mấu chốt của thuật toán, ý tưởng của này nhằm giúp chọn tâm cụm mới tránh gần (xa) với các tâm cụm đã có. Nếu $K = 2$ thì thuật toán đơn giản là chỉ khởi tạo 1 tâm cụm ngẫu nhiên ban đầu và tâm cụm 2 sẽ là điểm dữ liệu có khoảng cách xa nhất với tâm cụm vừa khởi tạo. Tiếp tục nếu $K > 2$ cụ thể $K = 3$ thì nó sẽ hay hơn rất nhiều, lúc này ta đã chọn 2 tâm cụm khá tốt về mặt không gian, tiếp theo ta tìm tập hợp dists bao gồm khoảng cách của mỗi điểm dữ liệu với tâm cụm gần nó nhất, chắc chắn rằng những điểm gần 2 tâm cụm ban đầu có giá trị cực nhỏ nhưng dữ liệu ở xa 2 tâm cụm ban đầu sẽ lớn, từ đây ta chỉ cần chọn điểm có khoảng cách lớn nhất làm tâm cụm mới.
Tới đây việc còn lại cho thuật toán K-means là cập nhật các centroids và nhãn cho điểm dữ liệu tương tự ở các phần trên.
6.2. Chọn số lượng cụm - Elbow method
Ở phần trên mình đã trình bày về cách cải tiến điểm khởi tạo của thuật toán K-means. Tuy nhiên, một điểm then chốt của thuật toán K-means đó là số lượng cụm cần được lựa chọn trước khi train/fit model. Với các ví dụ trình bày bên trên đều là các dữ liệu trong không gian 2D nên có thể dễ dàng nhìn bằng trực giác để đưa ra số lượng cụm, nhưng trong thực dữ liệu cao chiều thì không thể nhìn được.
Bạn có thể suy nghĩ rằng đưa ra số một số lượng cụm nhất định có thể là $K$ nằm trong khoảng [2, 10] và chọn ra giá trị $K$ có giá trị hàm cost nhỏ nhất, tuy nhiên nếu các điểm khởi tạo đã được tối ưu thì hàm cost sẽ luôn giảm khi số lượng cụm tăng. Đơn giản vì khi có càng nhiều cụm, khoảng cách những điểm gần nhau sẽ càng tập trung gần vào tâm cụm mà nó thuộc về và khoảng cách giữa tâm cụm và các điểm dữ liệu thuộc cụm đó ngày càng ngắn.
Phương pháp Elbow method sẽ giúp ta có thể chọn lựa số lượng cụm tốt hơn nếu ta chưa biết chọn số cụm như thế nào, hình ảnh minh họa:
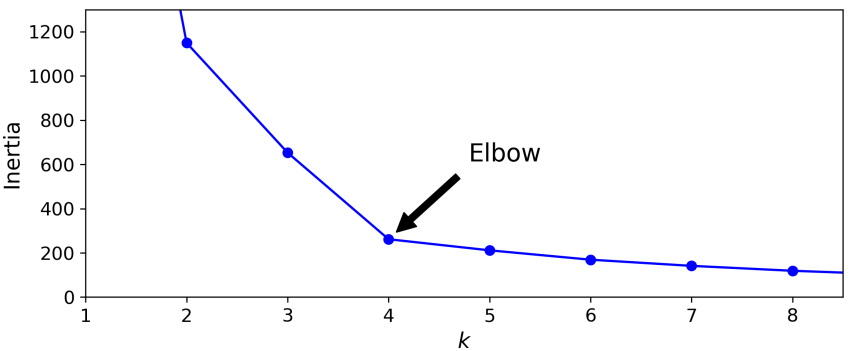
Hình 10: Elbow method
Ở hình 10, trục hoành là các giá trị $K$ (số cụm) và trục tung là giá trị inertia (cost function) tương ứng với $K$. Như đã thấy hướng của inertia đi nhanh, thẳng tới trước giá trị $K = 4$, sau đó $K$ tăng và hướng của inertia đi khá đều và chậm. Điều này chỉ ra rằng, giá trị inertia của giảm rất ít khi giá trị $K > 4$ tức hàm cost function không thay đổi gì nhiều, vì vậy ta có thể chọn số lượng cụm là 4 (tại điểm gấp khúc - khuỷu tay). Tuy nhiên trong một số trường nếu giá trị inertia giảm khá đều khi $K$ tăng thì sẽ khá khó để chọn $K$ chính xác. Có một phương pháp sử dụng để chọn số lượng cụm cũng khá phổ biến dựa trên silhouette score mà bạn có thể tham khảo thêm.
7. Đánh giá và kết luận
-
K-means là một thuật toán đơn giản, khá dễ để hiểu ý tưởng nhưng vẫn được ứng dụng khá nhiều trong các bài khác làm bước pre-processing. Hơn nữa, tuy thời gian để tính toán và suy ra nghiệm (tâm cụm) tốn thời gian, nhưng bù lại khi dự đoán lại rất nhanh.
-
Một số ứng dụng của K-means có thể kể tới là phân đoạn ảnh (Image Segmentation), Image Compression (nén ảnh) một lĩnh vực rất hay trong Computer Vision, giảm chiều dữ liệu, search engine, là tiền đề trong semi-supervised learning…
-
Tuy nhiên các điểm yếu về thuật toán có thể xử lí nhưng về dữ liệu thì khá khó như: K-means bị ảnh hưởng bởi nhiễu (outlier) vì dựa trên khoảng cách và giá trị trung bình để cập nhật tâm cụm, K-means sẽ đưa ra những kết quả khá kém trong trường hợp dữ liệu phân chia theo kiểu đường viền hình tròn, dẹt hay trong các tập dữ liệu bị mất cân bằng về phân phối mỗi cụm…
-
Ngoài ra có một số điểm khá hay của thư viện scikit-learn với K-means mà mình chưa đề cập tới, bạn có đọc documents của K-measn trong sklearn tại đây.
8. Tham khảo
[1] Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow
[2] Bài 4: K-means Clustering - Machine Learning cơ bản by Vu Huu Tiep
